Mathematik Dreisatz

Proportionaler Dreisatz:
Je mehr (weniger) von einer Größe umso mehr (weniger) von der anderen Größe

Bsp.: 3kg Äpfel kosten 4,80 €, wieviel kosten 5,5kg

Je mehr Äpfel umso mehr €. Also proportionaler Dreisatz.
Man ordnet die Daten in ein sinnvolles System. Pro Zeile jeweils eine Größe, hier € und kg, wobei man mit der unbekannten Größe x oben beginnt

Nun zieht man Bruchstriche und setzt beide Seiten gleich

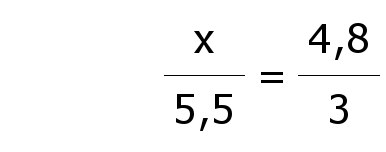
Multiplikation mit 5,5 liefert das Ergebnis.

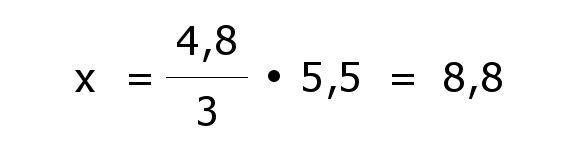
Antiproportionaler Dreisatz:
Je mehr (weniger) von einer Größe umso weniger (mehr) von der anderen Größe

Bsp.: Drei Pumpen füllen ein Schwimmbecken in 7 Stunden. In welcher Zeit ist das Schwimmbecken gefüllt wenn 5 Pumpen verwendet werden.

Je mehr Pumpen umso weniger Stunden. Also antiproportionaler Dreisatz.
Man ordnet die Daten in ein sinnvolles System. Pro Zeile jeweils eine Größe, hier Stunden und Pumpen, wobei man mit der unbekannten Größe x oben beginnt

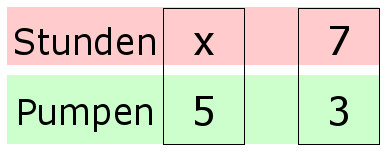
Nun multipliziert man die Spaltenwerte und setzt beide Seiten gleich

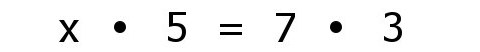
Division mit 5 liefert das Ergebnis.

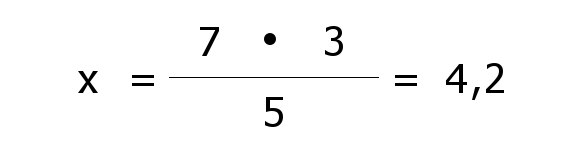
Ergebnis 4,2 Stunden. Wieviel Minuten sind 0,2 Stunden?
Dies ist ein portionaler Dreisatz:

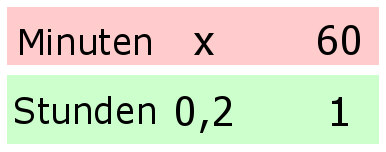
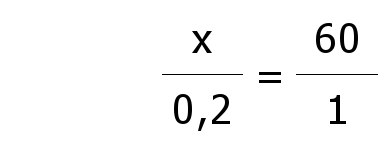
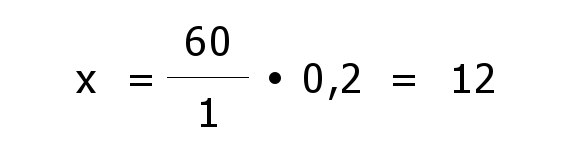
Das Endergebnis also 4 Stunden und 12 Minuten.

Zusammengesetzter Dreisatz:

Ein klassisches Bsp.: Zwölf Einschaler haben bei 9-stündiger Arbeitszeit in 7 Tagen 390 m² Betonschalung hergestellt. Wieviele Einschaler sind (bei gleicher Leistung) einzusetzen, damit in 21 Tagen 2340 m² Betonschalung hergestellt werden wobei die tägliche Arbeitszeit nur 8 Stunden beträgt?

Man ordnet die Daten in ein sinnvolles System. Pro Zeile jeweils eine Größe, wobei man mit der unbekannten Größe x oben beginnt

Nun betrachtet man neben der ersten Zeile (Einschaler, rosa) nur eine weitere Zeile, z.B. die zweite Zeile (m², grün). Die anderen Zeilen bleiben unberücksichtigt. Es liegt ein proportionaler Dreisatz vor:

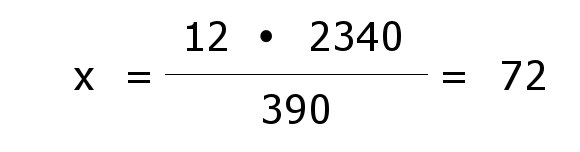
Die Aufgabe reduziert sich zu

Nun betrachtet man neben der ersten Zeile (Einschaler, rosa) wieder nur eine weitere Zeile, z.B. die dritte Zeile (Arbeitsstunden, blau). Die anderen Zeilen bleiben unberücksichtigt. Es liegt ein antiproportionaler Dreisatz vor:

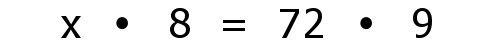
Mit der Lösung x=81 reduziert sich die Aufgabe zu

Nun betrachtet man neben der ersten Zeile (Einschaler, rosa) nur noch die übrig gebliebene Zeile (Tage, gelb). Die anderen Zeilen sind schon auf die gewünschten Werte umgeschrieben worden. Es liegt ein antiproportionaler Dreisatz vor:

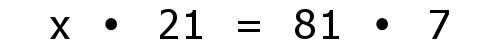
Das Endergebnis lautet also 27 Einschaler.

Bei einem proportionalen Dreisatz ist das Verhältnis einer Größe y und einer anderen Größe x immer konstant. y/x = a oder y =a . x Dies ist graphisch gesehen die Gleichung einer Geraden durch den Ursprung

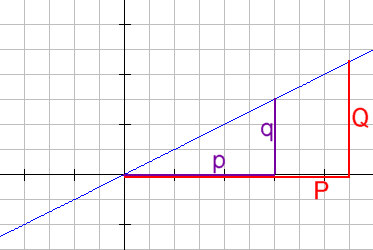
Daher hat man q/p = Q/P was geometrisch ein Strahlensatz ist.
Sieht man es geometrisch so hat man ein rechtwinkliges Dreieck

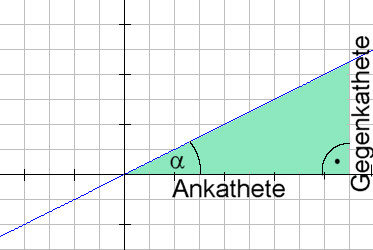
und damit die Aussage daß das Verhältnis von Gegenkathete/Ankathete immer konstant ist. Man kann es damit dem Winkel Alpha zuordnen und diese Zuordnung nennt man Tangens

Gegenkathete/Ankathete = tan

Es ist sofort klar daß
tan 45° = 1
tan 0° = 0
tan 90° = unendlich
ist. Für andere Werte nimmt man den Taschenrechner.