Mathematik

Mathematik a = b

Zitat aus C. G. Jung "Erinnerungen, Träume, Gedanken":
"Am meisten empörte mich der Grundsatz: wenn a=b und b=c dann ist a=c, wo es doch per definitionem feststand, daß a etwas anderes bezeichnete als b und daher als etwas anderes nicht mit b gleichzusetzen war, geschweige denn mit c. Wenn es sich um eine Gleichsetzung handelt, dann heißt sie a=a, b=b usw., während a=b mir direkt als Lüge oder Betrug vorkam."
In der Mathematik sind a, b, c, usw. Abkürzungen für Sinneinheiten, etwa
a=1Stunde
b=60Minuten
c=3600Sekunden
a steht als Abkürzung für die Zeitdauer von einer Stunde, nicht als Gleichheit der Zeichen an sich. Es gilt
1Stunde=60Minuten abgekürzt a=b
60Minuten=3600Sekunden   abgekürzt b=c
Dann kann man folgern daß a=c ist, also 1Stunde=3600Sekunden.
Anderes Beispiel bei dem eine Division ausgeführt wird

        1:9=0,1111111111...

Nun ist eine Zahl durch ... nicht genau genug beschrieben, denn es könnte sein daß nach der 2400-ten Stelle auf einmal eine 5 erscheint. Man weiß aber daß dies nicht der Fall sein wird und schreibt zum genaueren Erfassen des Sachverhaltes einen Strich über die 1, was bedeuted daß diese 1 sich immer wiederholt

        1:9 = 0,1
Die rechte und die linke Seite haben deutlich abweichende Zeichenfolgen, links gibt es ein Geteilt-Zeichen und 9 während es rechts ein Komma und eine 1 gibt, die als periodische Wiederholung gekennzeichnet ist. Diese unterschiedlichen Ausdrücke können abstrakt mit verschiedenen Buchstaben bezeichnet werden
a= 1:9
b= 0,1
und man kann rechnen

Nun muß man sich in der Mathematik an feste Regeln halten. Eine Regel lautet

wenn a=b dann auch ma=mb

Das heißt ausführlich: wenn zwei Größen gleich sind so sind auch die Vielfachen mit dem Multiplikator m dieser Größen gleich.
Also ist 9a=9b oder

Normalerweise denkt man über diese Regeln nicht nach und schreibt

Eine weitere Regel wurde oben noch benutzt. Das Multiplikationszeichen zwischen zwei Größen braucht man nicht zu schreiben, solange der Ausdruck verständlich ist. Daher wird niemand im folgenden Beispiel das Multiplikationszeichen weglassen und schreiben:

Aber eine andere Zweideutigkeit ist in ständigem Gebrauch

In der Mathematik ist der linke Ausdruck richtig, z.B. 2

½ für den Umfang eines Kreises mit Radius ½. Im kaufmännischen Rechnen und im täglichen Gebrauch ist oft der rechte Ausdruck gemeint, z.B. Dreieinhalb Pfund Kartoffeln. Welcher der beiden Sinneinheiten gemeint ist kann man nur in dem Zusammenhang erkennen. Es ist ähnlich wie mit dem Wort Maus, das die Maus bezeichnet die den Käse frißt, oder auch die Computer-Maus. Erst im Zusammenhang ergibt sich die Bedeutung.

Eine andere Regel ist
a + b = b + a
Das heißt ausführlich: Die Reihenfolge bei der Addition ist gleichgültig. Der Mathematiker Carl Friedrich Gauß hat als Schuljunge im Alter von 9 Jahren diese Regel benutzt um eine Aufgabe zu lösen die sinngemäß die Form hat:
Man addiere alle positiven ganzen Zahlen von 1 bis 1000.

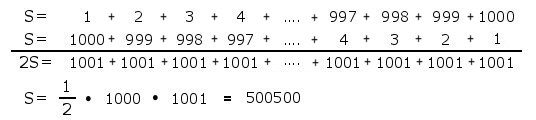
Die Zahlen wurden ein zweites Mal in umgekehrter Reihenfolge unter die ursprüngliche Zahlenfolge geschrieben. Dann wurde spaltenweise addiert.

Natürlich gilt NICHT daß a - b gleich b - a ist. Und auch
a + b = b + a
gilt nicht in jedem Fall. Dazu kann man einen kaufmännischen Taschenrechner nehmen und eintippen:

Es ist also 11+7x4 NICHT gleich 7x4+11, bei der Verwendung eines kaufmännischen Taschenrechners.
Der Grund ist daß der kaufmännische Taschenrechner nach anderen Regeln programmiert wurde. Es wird nach jeder Rechenoperation gleich eine Zwischensumme gebildet und es gilt nicht die Regel Punkt-vor-Strich, d.h. die Multiplikation bindet NICHT stärker als die Addition. Bei einem kaufmännischen Taschenrechner rechnet man am besten Multiplikation und Division im normalen Zählwerk und tippt mit M+ und M- die Addition/Subtraktion in den Speicher. Wichtig ist also immer die Regeln zu kennen.
Bei einem wissenschaftlichen Taschenrechner wird Punkt-vor-Strich berücksichtigt und die obigen Taschenrechner-Eingaben führen zum gleichen Ergebnis. Wie sieht es beim wissenschaftlichen Taschenrechner mit folgender Aufgabe aus. Eintippen der Zahlen/Operationen nach der üblichen Lese-Regel: von links nach rechts lesen und von oben nach unten:

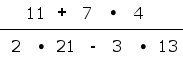
liefert ein falsches Ergebnis. Der Taschenrechner berücksichtigt Punkt-vor-Strich und rechnet zuerst den rosa markierten Bereich und addiert und subtrahiert die anderen Elemente. Hier wurde die Regel vergessen daß beim Bruchstrich gilt: alles was oben steht wird durch alles was unten steht geteilt, also sind Klammern zu bilden

Aber wie genau rechnet der Taschenrechner in diesem Fall den rosa markierten Bereich? Dazu die folgende Aufgabe §A

Es ist suggestiv die Kombination 2

als Einheit aufzufassen und als Ergebnis der Aufgabe §A den Wert 5 anzugeben. Aber man darf nicht vergessen daß diese Kombination
2 mal

bedeuted und das Eintippen im Taschenrechner oder in einer Tabellenkalkulation führt zu folgendem Resultat
(sofern man für

den Näherungswert 3,14 verwendet)

Die Aufgabe §A ist nicht eindeutig formuliert:

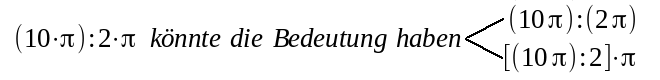
Taschenrechner und Tabellenkalkulation richten sich nach der unteren Möglichkeit. Ganz ähnlich ist es bei der Aufgabe §B

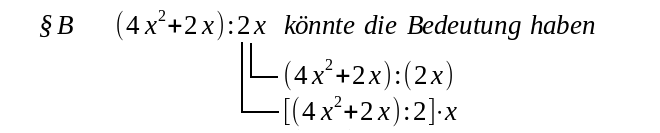
Natürlich erhält man ganz unterschiedliche Ergebnisse. Entweder muß man diese Aufgabe eindeutig formulieren oder man muß sich an die Regel halten die der Lehrer zum Bearbeiten dieses Aufgabentyps vorgegeben hat.

Wenn man nicht immer überlegt welche Regel man anwendet kann es leicht zu einem Fehler kommen:

Hier ist natürlich ein Fehler gemacht worden. Die folgende Regel ist nicht beachtet worden: Das Multiplikationszeichen zwischen zwei Größen braucht man nicht zu schreiben, solange der Ausdruck verständlich ist.
Es sind 10ct gleich zehn mal ein cent (man denke an Münzen).
Daher ist richtig:

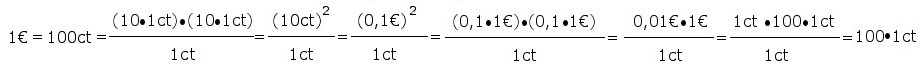
Die Regeln ganz ausführlich
1)=: 1€=100 x 1ct =10 x 10 x 1ct
2)=: ab/b=a mit a=10 x 1ct x 10 und b=1ct ,Regel für das Kürzen/Erweitern
und ab=ba, Reihenfolge der Multiplikation ist gleichgültig
3)=: aa=a² mit a=10 x 1ct =10ct
4)=: 10ct=0,1 x 100 x 1ct =0,1€
5)=: a²=aa mit a=0,1 x 1€ =0,1€
6)=: ab=ba, Reihenfolge der Multiplikation ist gleichgültig
7)=: 1€=100 x 1ct
8)=: ab/b=a mit a =0,01€ x 100 und b=1ct ,Regel für das Kürzen/Erweitern und ab=ba, Reihenfolge der Multiplikation ist gleichgültig

Vielleicht noch ein Wort zur Situation in der realen Welt

Nun gibt es neue Autos, schmutzige Autos, Autos mit einer Beule im Blech, jede Menge Fabrikate und wenn man Vergleiche anstellt bis hin zur atomaren Ebene, so kann man die Meinung vertreten daß es nirgendwo zwei genau gleiche Autos gibt. Müßte man somit nicht schreiben: