Mathematik

Geometrie in alten Kulturen

Geometrische Vorstellungen für mathematische Sachverhalte waren schon seit langem in alten Kulturen vorhanden und lassen einige Dinge sehr anschaulich begreifbar machen.

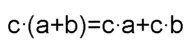
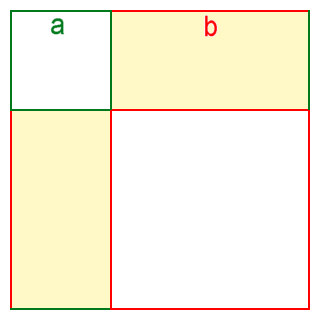
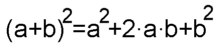Dies ist eine der binomischen Formeln

Nun kann man einwenden, daß man die Ausdrücke in Klammern auch einfach ausmultiplizieren kann. Aber man muß beachten, daß die Regeln für das Ausmultiplizieren abgeleitet werden von einigen grundlegenden Annahmen (nicht weiter zu beweisenden Axiomen und Definitionen) und dazu gehört auch

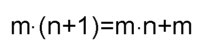für natürliche ganze Zahlen m und n
Mit den obigen Bildern kann man diese Definition anschaulich und plausibel machen. Und ich denke daß obige Gleichungen aus den Bildern genauso anschaulich und plausibel als wahr zu verstehen sind für beliebige reelle Zahlen.

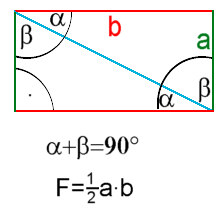
Denkt man sich nun ein Rechteck mit den Seiten a und b und teilt dieses diagonal so entstehen 2 gleich große Dreiecke, die jeweils einen rechten Winkel besitzen (90°).
Es ist anschaulich für ein solches Dreieck:
Die Summe aller drei Winkel beträgt 180°
Die Fläche beträgt die Hälfte der Fläche des Rechteckes.

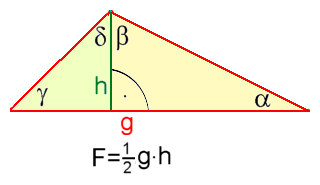
Ist es ein Dreieck ohne rechten Winkel so zieht man vom höchsten Punkt eine Senkrechte auf die Grundseite. Dadurch zerlegt man das Dreieck in zwei rechtwinklige Dreiecke (gelbe und grüne Fläche).
Es ist anschaulich für ein solches Dreieck:
Die Summe aller drei Winkel beträgt 180°
Die Fläche beträgt die Hälfte der Fläche von Grundseite mal Höhe.

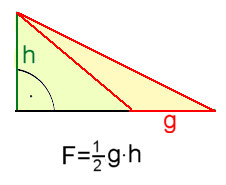
Ist das rote Dreieck anders positioniert so zieht man vom höchsten Punkt eine Senkrechte auf die waagrecht verlängerte Grundseite. Von dem Dreieck grün+gelb subtrahiert man das grüne Dreieck.
Das Ergebnis ist für das rote Dreieck wieder:
Die Summe aller drei Winkel beträgt 180°
Die Fläche beträgt die Hälfte der Fläche von Grundseite mal Höhe.

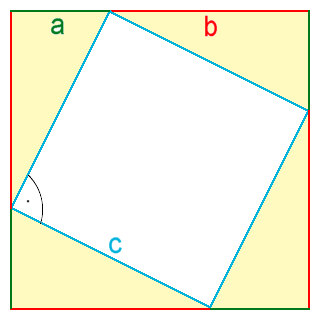
Nach den obigen Überlegungen beim Dreieck sieht man daß das innere Vierseiten-Objekt rechte Winkel besitzt.
Setzt man B=(a+b)² - 2ab
so zeigt die linke Figur c²=B
Nach der obigen binomischen Formel gilt
B=a²+b²
Damit hat man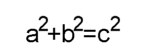

Der Satz des Pythagoras.
Hierbei wurden nur Flächenvergleiche durchgeführt und der Klammerausdruck nicht wirklich ausmultipliziert.

Bei einem rechtwinkligen Dreieck ist die Seite die dem rechten Winkel gegenüberliegt die längste Seite und man kann diese als Grundseite verwenden. Fällt man das Lot vom höchsten Punkt so wird die Grundseite in die Abschnitte q und p geteilt.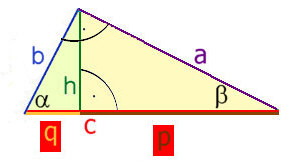

Das Verhältnis von Gegenkathete/Ankathete (tangens) ist immer konstant. Daher bei dem Winkel

für das grüne Dreieck und das grüne+gelbe Dreieck
h/q = a/b
und bei dem Winkel

für das gelbe und das grüne+gelbe Dreieck
h/p=b/a
Daher folgt
h² = pq
Das ist der Höhensatz.
Das Verhältnis von Ankathete/Hypotenuse (cosinus) ist ebenfalls eine Konstante. Daher bei dem Winkel

für das grüne Dreieck und das grüne+gelbe Dreieck
b² = cq
und bei dem Winkel

für das gelbe und das grüne+gelbe Dreieck
a² = cp
Das ist der Kathetensatz des Euklid.
Und damit
a²+b² = c(p+q) = c²

Nimmt man jetzt ein Koordinatensystem und bestimmt alle Punkte (x,y) für die gilt
x²+y²=r²
so erhält man die Punkte auf einem Kreis mit Radius r.
Hier wurde auch gleich ein zweiter Kreis mit Radius R eingezeichnet.

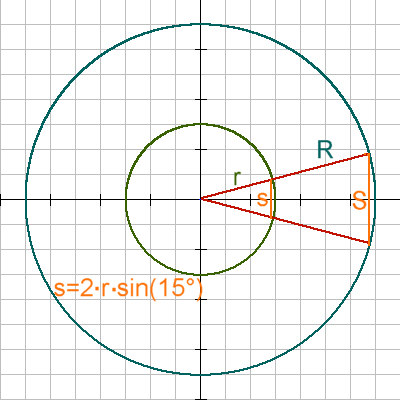
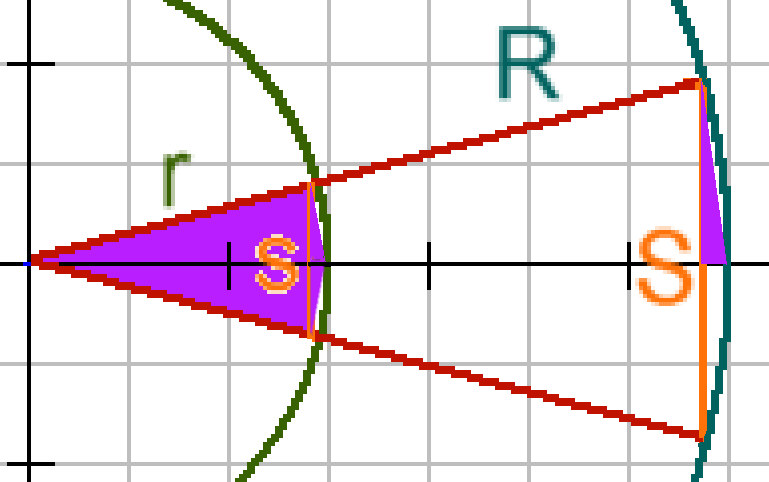
Man teile den kleinen Kreis gedanklich in 12 aneinanderliegende Kreisausschnitte (also 360°/12). Im Bild wurde ein solcher Kreisausschnitt gezeichnet. Die orange Strecke nahe am Kreisbogen nähert sich grob der Länge des Kreisbogens an. Durch das 12-fache davon erhält man eine grobe Näherung des Kreisumfanges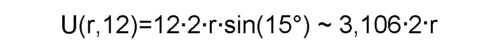

Mit einem Taschenrechner läßt sich das schnell ausrechnen.
Erhöht man die Anzahl der aneinanderliegenden Kreisausschnitte, z.B. 1200
so erhält man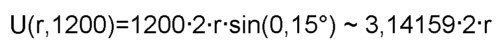

Mit weiterer Erhöhung der Anzahl der aneinanderliegenden Kreisausschnitte werden die Ergebnisse immer genauer, d.h. die Anzahl der Stellen hinter dem Komma die sich nicht verändern wird immer größer. Damit kann man das Ergebnis beliebig genau berechnen.
Betrachtet man jetzt beide Kreise so ergibt ein Strahlensatz
s/r =S/R und damit auch U(r,1200)/r = U(R,1200)/R
Denkt man sich die Anzahl beliebig groß so erhält man die Aussage, daß das Verhältnis von Umfang/Radius für jeden Kreis gleich groß ist.
Historisch wurde der Durchmesser des Kreises benutzt um dieser Konstanten einen Namen zu geben
Kreisumfang=Kreisdurchmesser x

Und oben wurde

näherungsweise berechnet zu 3,14159

Solche Überlegungen kann man auch durchführen um den Flächeninhalt des Kreises zu bestimmen. Dazu kann man die waagrechte Grundseite auf r vergrößern um das lila Dreieck über der schwarzen Linie zu erhalten. Und für dieses ist der Flächeninhalt dann Grundseite=r multipliziert mit der Höhe=s/2 multipliziert mit 1/2.

Bei 12 aneinanderliegenden Kreisausschnitten erhält man die angenäherte Fläche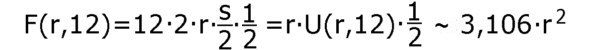

Erhöht man die Anzahl der aneinanderliegenden Kreisausschnitte, z.B. 1200 so erhält man

Mit weiterer Erhöhung der Anzahl der aneinanderliegenden Kreisausschnitte über alle Vorstellungen hinaus ergibt sich für einen Kreis mit Radius r

Es gibt vielleicht einen Einwand gegen das Verwenden des Taschenrechners weil dieser bei der Umwandlung von Gradmaß zu Bogenmaß die Zahl

ben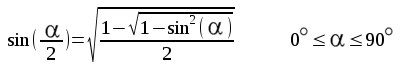utzt und man daher eine Näherungsrechnung der Zahl

nicht machen kann wenn man

schon bei der programmierten Berechnung des Taschenrechners verwendet. Aber man kann Berechnungen durchführen ohne die Taste mit sinus beim Taschenrechner zu drücken. Man weiß

und

Folglich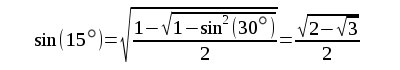

Man kann diesen sinus-Wert durch Wurzelausdrücke berechnen. Und wenn man ständige Halbierungen durchführt so kann man beliebig kleine Winkel durch Wurzelausdrücke berechnen, z.B.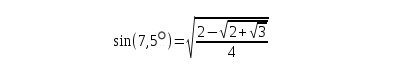

oder in der Folge die Werte
3,75
1,875
0,9375
0,46875
0,234375
und bei
U(r,1536) bekommt man mit der Berechnung von 1536xsin(0,1171875°) alleine über Wurzelausdrücke die oben angegebene Genauigkeit von

mit 5 Stellen hinter dem Komma.

Nun muß man natürlich bei geometrischen Überlegungen vorsichtig sein. Ein bekanntes Beispiel dafür ist der "geometrische Beweis" von 64=65

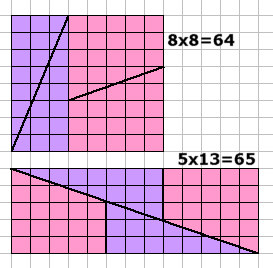
Aber schon mit dem Strahlensatz erkennt man den hier gemachten Fehler.

Wie sieht es nun in der realen Welt aus.
Die geometrischen Verhältnisse wurden durch Abstraktion aus der realen Welt gewonnen. Zugrundegelegt wurde z.B. die Existenz von Punkten, Linien, ebenen Flächen und Längen.
Nun ist die wirkliche Darstellung eines Punktes in der realen Welt eigentlich gar nicht möglich. Macht man etwa einen Punkt auf ein Blatt Papier so ist dies unter dem Mikroskop ein unregelmäßiger Fleck. Macht man diesen Fleck immer kleiner so wird dieser nur mit aufwendigen Hilfsmitteln sichtbar (und ist immer noch kein Punkt) und für eine Verwendung im realen Leben nicht mehr zu gebrauchen. Im realen Leben verwendet man sinnvolle Näherungen des Begriffs Punkt.
Eine ebene Fläche ist in der realen Welt auch nicht möglich. Betrachtet man ein Blatt Papier unter dem Mikroskop so sieht es aus wie eine Gebirgslandschaft. Es erscheint uns auch eine Wasserfläche als ebene Fläche, aber die Wasserfläche ist ein Ausschnitt der Oberfläche der Erdkugel die durch die Anziehungskraft des Mondes und die Gestalt der Erdoberfläche keinesfalls einer gedanklichen Kugel entspricht und schon gar nicht eben ist (die Erde ist keine Scheibe).
Bei einer Linie ist es ähnlich. Man muß einen sichtbaren Strich ziehen der dann eine gewisse Breite besitzt und unter dem Mikroskop einer holprigen ausgefransten Straße gleicht. Oder man nimmt einen Lichtstrahl den man durch ein kleines Loch schickt und erkennt daß durch Beugung und der unregelmäßigen Randform des Loches (bei Betrachtung unter dem Mikroskop) der Strahl aufgefächert wird.
Auch eine Länge wie den Meter kann man nur näherungsweise realisieren. Man vergleiche dazu ein Zitat Wikipedia:
Die Länge des Meters wurde festgelegt als der Abstand der Mittelstriche zweier Strichgruppen auf dem auf einer konstanten Temperatur von 0 °C gehaltenen Stab. Es wurden 30 Kopien dieses Prototyps hergestellt und an nationale Eichinstitute übergeben. Obgleich bei der Herstellung der Meterprototypen größter Wert auf Haltbarkeit und Unveränderbarkeit gelegt worden war, war doch klar, dass diese grundsätzlich vergänglich sind. Die Anfertigung von Kopien führte zwangsläufig zu Abweichungen und - ebenso wie regelmäßige Vergleiche der Kopien untereinander und mit dem Original - zum Risiko von Beschädigungen.
Eine neue Definition über die Wellenlänge wurde eingeführt. Dazu wird die Wellenlänge eines Atomes (entstanden aus bestimmten Zustandsänderungen des Atomes) im Vakuum zugrundegelegt. Aber ist ein 100%-iges Vakuum möglich, ist eine 100%-ige Reinheit der gebrauchten Atome möglich, sind nicht aufwändige Apparaturen dazu nötig (mit näherungsweise produzierten Teilen), ist dazu nicht ein umfangreiches Gedankengebäude notwendig. Hilft dies im realen Leben wirklich wenn man eine im Baumarkt gekaufte Latte auf 2m Länge zuschneiden will.
Jedenfalls ist es im realen Leben so daß alles nur näherungsweise erfaßt werden kann. Und es ist doch erstaunlich wie abstrakte Vorstellungen wie die obigen geometrischen Vorstellungen durch technische Anwendungen in der realen Welt gewaltige Veränderungen bewirkt haben.