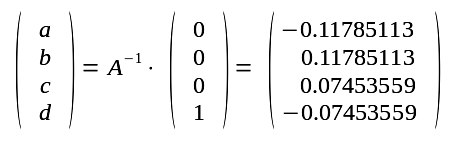|
Matrix, Vektor, Inverse
Die Ausführungen der
vorherigen Seiten über Programmfenster, insbersondere die Seite Man kann sich mit dem Problem von n Gleichungen mit n Unbekannten beschäftigen. Hier wird nur etwas über den Fall n=4 aufgeschrieben |

|
Man bezeichnet das Zahlenschema unten links als Matrix. Es ist eine Art
Tabelle für die Rechenoperationen festgelegt werden. Die anderen beiden
spaltenartigen Objekte bezeichnet man als Vektoren. Durch die Herleitung
weiß man wie die Multiplikation einer Matrix mit einem Vektor
funktionieren muß: Es wird eine Zeile der Matrix mit dem Vektor
verknüpft, indem eine Zahlenmultiplikation der Positionselemente erfolgt
und dann alles aufaddiert wird. Eine solche Positionsmultiplikation
erfolgt auch bei while read so daß das Terminal diese Problematik elegant bewältigen kann. Für das Terminal ist die Matrix und der Vektor jeweils einfach eine Variable. Es wird ein zenity-Fenster aufgeschrieben, das aus der Matrix eine Variable macht. Dabei werden mögliche Kommas in Punkte übersetzt, denn es gibt bestimmt auch Kommazahlen bei der Eingabe. Weiter werden mögliche Tabulatorzeichen in Leerzeichen verwandelt. |
| MA01=$(echo "$(zenity --entry --ok-label "EINGABE" --title "EINGABE-FENSTER" --text " Bitte 4x4-Matrix eingeben")" | sed 's/,/\./g' | sed 's/\t/ /g') |
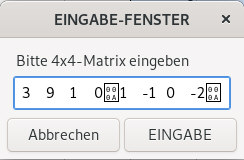
| Die Werte kann man aus einem Tabellenprogramm oder einem Writer-Dokument in das Eingabefeld kopieren |
| Im Eingabefeld erscheinen eigenartige Zeichen die für den Zeilenumbruch stehen und die man nicht weiter beachten muß. |
| echo "$MA01" |
|
1 7 1 2 0 1 1 1 3 9 1 0 1 -1 0 -2 Als nächstes wird ein Eingabefenster für den Vektor aufgeschrieben, und auch hier wird in das Eingabefeld hineinkopiert: |
| Vv=$(echo "$(zenity --entry --ok-label "EINGABE" --title "EINGABE-FENSTER" --text " Bitte 4-zeiligen Vektor eingeben")" | sed 's/,/\./g') |
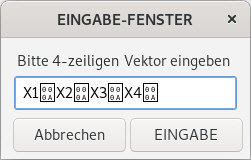
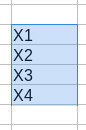
| echo "$Vv" |
|
X1 X2 X3 X4 Nun werden die beiden Variablen aneinandergeklebt, wobei zuvor die Matrix-Variable transponiert wird |
| suA4=$(paste -d " " <(echo "$MA01" | sed 's/ /\n/g'| pr -t -s" " -4) <(echo "$Vv")) |
| echo "$suA4" |
|
1 0 3 1 X1 7 1 9 -1 X2 1 1 1 0 X3 2 1 0 -2 X4 Nun wird while read aufgerufen und zum Schluß alles wieder zurücktransponiert |
| while read MZ1 MZ2 MZ3 MZ4 Vektor; do echo "$MZ1*$Vektor $MZ2*$Vektor $MZ3*$Vektor $MZ4*$Vektor"; done <<< $(echo "$suA4") | sed 's/ /\n/g'| pr -t -s"+" -4 |
|
1*X1+7*X2+1*X3+2*X4 0*X1+1*X2+1*X3+1*X4 3*X1+9*X2+1*X3+0*X4 1*X1+-1*X2+0*X3+-2*X4 Man erhält also die Berechnung der Multiplikation einer 4x4-Matrix MA01 mit dem Vektor Vv. Es ergeben sich einige vorzeichenbedingten Unklarheiten. Dazu kann man im Terminal berechnen: |
| echo "1+-2*-3" | bc |
|
Es zeigt sich daß 1+-2*-3 bei der Berechnung die Bedeutung 1+(-2)*(-3) hat und genauso sollte es sein. Damit kann man ein kleines script schreiben zum Multiplizieren einer 4x4-Matrix mit einem 4-zeiligen Vektor. Das script wird wieder in dem Ordner ~/Bla abgelegt: |
| nano ~/Bla/4x4-Matrix-mal-Vektor.sh |
| Eingabe in den Editor |
|
#!/bin/bash MA=$(zenity --entry --ok-label "EINGABE" --title "EINGABE-FENSTER" --text " Bitte 4x4-Matrix eingeben") if [ $? -ne 0 ]; then exit fi MA01=$(echo "$MA" | sed 's/,/\./g' | sed 's/\t/ /g') if [ $(echo "$MA01" | wc -l) -ne 4 ]; then zenity --info --width="280" --title="Fehler" --text "Matrix\n\n ist nicht vom Typ 4x4" exit fi if [ $(echo "$MA01" | head -n 1 | sed 's/ /\n/g' | wc -l) -ne 4 ]; then zenity --info --width="280" --title="Fehler" --text "Matrix\n\n ist nicht vom Typ 4x4" exit fi V=$(zenity --entry --ok-label "EINGABE" --title "EINGABE-FENSTER" --text " Bitte 4-zeiligen Vektor eingeben") if [ $? -ne 0 ]; then exit fi Vv=$(echo "$V" | sed 's/,/\./g') if [ $(echo "$Vv" | wc -l) -ne 4 ]; then zenity --info --width="280" --title="Fehler" --text "Spaltenvektor\n\n ist nicht 4-zeilig" exit fi suA4=$(paste -d " " <(echo "$MA01" | sed 's/ /\n/g'| pr -t -s" " -4) <(echo "$Vv")) suA5=$(while read MZ1 MZ2 MZ3 MZ4 Vektor; do echo "$MZ1*$Vektor $MZ2*$Vektor $MZ3*$Vektor $MZ4*$Vektor"; done <<< $(echo "$suA4") | sed 's/ /\n/g'| pr -t -s"+" -4 | bc -l | sed 's/^0$/0.0/' | sed -r 's/^(-?)\./\10./' | sed -r 's/(\.?)0*$//') zenity --text-info --title="Ergebnis der Multiplikation von 4x4-Matrix mit dem Vektor" --width=480 --height=200 <<< $suA5 |
| Nun muß man das script ausführbar machen. |
| chmod +x ~/Bla/4x4-Matrix-mal-Vektor.sh |
|
Setzt man A=MATRIX und X=Vektor mit den Unbekannten und B=Vektor mit den Werten auf der rechten Seite, so schreibt sich das Problem mit den 4 Gleichungen mit 4 Unbekannten |
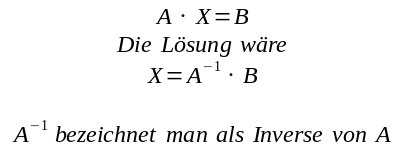
|
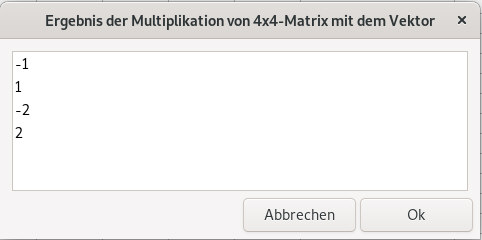
Die inverse Matrix von A lautet -8.5 3 5.5 -7 2.5 -1 -1.5 2 3 0 -2 3 -5.5 2 3.5 -5 Setzt man für B die Werte 8 1 4 -6 und kopiert dies bei Aufruf des scriptes 4x4-Matrix-mal-Vektor.sh ein so erhält man |
|
Die Lösungen des obigen Gleichungssystems sind also X1=-1 X2=1 X3=-2 X4=2 Es bleibt die Frage wie man die Inverse einer Matrix bestimmt. Dazu gibt es einen Lösungsweg von Gauß-Jordan der sich gut in bash umsetzen läßt. Zunächst einige Vorbemerkungen. Es wird eine allgemeine 4x4-Matrix erstellt. S steht für Spalte Z steht für Zeile |
| A=$(echo Z{1..4}S{1..4} | sed 's/ /\n/g' | pr -at -s" " -4) |
| echo "$A" |
|
Z1S1 Z1S2 Z1S3 Z1S4 Z2S1 Z2S2 Z2S3 Z2S4 Z3S1 Z3S2 Z3S3 Z3S4 Z4S1 Z4S2 Z4S3 Z4S4 Nun soll bei der MATRIX A das Element in der Zeile z und der Spalte s herausgefiltert werden: MATRIXelementZEILEzSPALTEs=$(echo "$A" | cut -d " " -f s | head -n z | tail -n 1) z.B.: |
| MATRIXelementZEILE3SPALTE2=$(echo "$A" | cut -d " " -f 2 | head -n 3 | tail -n 1) |
| echo "$MATRIXelementZEILE3SPALTE2" |
|
Z3S2 Einheitsmatrix erzeugen |
| Ee=$(echo -e "1 0 0 0\n0 1 0 0\n0 0 1 0\n0 0 0 1") |
| echo "$Ee" |
|
1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 Nun wird ein kleines script geschreiben um die Inverse einer 4x4-Matrix zu bestimmen. Das script wird wieder in dem Ordner ~/Bla abgelegt: |
| nano ~/Bla/4x4-Matrix-invertieren.sh |
| Eingabe in den Editor |
|
#!/bin/bash MA=$(zenity --entry --ok-label "EINGABE" --title "EINGABE-FENSTER" --text " Bitte 4x4-Matrix eingeben") if [ $? -ne 0 ]; then exit fi MA01=$(echo "$MA" | sed 's/,/\./g' | sed 's/\t/ /g') if [ $(echo "$MA01" | wc -l) -ne 4 ]; then zenity --info --width="280" --title="Fehler" --text "Matrix\n\n ist nicht vom Typ 4x4" exit fi if [ $(echo "$MA01" | head -n 1 | sed 's/ /\n/g' | wc -l) -ne 4 ]; then zenity --info --width="280" --title="Fehler" --text "Matrix\n\n ist nicht vom Typ 4x4" exit fi MA12=$(paste -d " " <(echo "$MA01") <(echo -e "1 0 0 0\n0 1 0 0\n0 0 1 0\n0 0 0 1") | sed 's/ /\n/g' | pr -t -s" " -4) for i in {1..4}; do read MA12$i <<< $(echo "$MA12" | cut -d " " -f $i | head -n 1 | tail -n 1 | sed 's/-//g'); done Ss4=$(echo "($MA121 + $MA122 + $MA123 + $MA124)*100000000000000/4" | bc -l | cut -f 1 -d '.' ) if [ $Ss4 -eq 0 ]; then zenity --info --width="280" --title="Fehler" --text "Matrix\n\n ist nicht invertierbar" exit fi if [[ $(echo "100000000000000*$MA121/1" | bc) -gt $Ss4 ]]; then MA02=$(echo "$MA12") else if [[ $(echo "100000000000000*$MA122/1" | bc) -gt $Ss4 ]]; then MA02=$(while read MZ1 MZ2 MZ3 MZ4; do echo "$MZ2 $MZ1 $MZ3 $MZ4"; done <<< $(echo "$MA12")) else if [[ $(echo "100000000000000*$MA123/1" | bc) -gt $Ss4 ]]; then MA02=$(while read MZ1 MZ2 MZ3 MZ4; do echo "$MZ3 $MZ2 $MZ1 $MZ4"; done <<< $(echo "$MA12")) else MA02=$(while read MZ1 MZ2 MZ3 MZ4; do echo "$MZ4 $MZ2 $MZ3 $MZ1"; done <<< $(echo "$MA12")) fi fi fi MA13=$(while read MZ1 MZ2 MZ3 MZ4; do for i in {1..4}; do read MA02$i <<< $(echo "$MA02" | cut -d " " -f $i | head -n 1 | tail -n 1); done ; echo "$MZ1 $(echo "scale=30; $MZ2*$MA021 - $MZ1*$MA022" | bc -l) $(echo "scale=30; $MZ3*$MA021 - $MZ1*$MA023" | bc -l) $(echo "scale=30; $MZ4*$MA021 - $MZ1*$MA024" | bc -l)"; done <<< $(echo "$MA02")) for i in {2..4}; do read MA13$i <<< $(echo "$MA13" | cut -d " " -f $i | head -n 2 | tail -n 1 | sed 's/-//g'); done Ss3=$(echo "($MA132 + $MA133 + $MA134)*100000000000000/3" | bc -l | cut -f 1 -d '.' ) if [ $Ss3 -eq 0 ]; then zenity --info --width="280" --title="Fehler" --text "Matrix\n\n ist nicht invertierbar" exit fi if [[ $(echo "100000000000000*$MA132/1" | bc) -gt $Ss3 ]]; then MA03=$(echo "$MA13") else if [[ $(echo "100000000000000*$MA133/1" | bc) -gt $Ss3 ]]; then MA03=$(while read MZ1 MZ2 MZ3 MZ4; do echo "$MZ1 $MZ3 $MZ2 $MZ4"; done <<< $(echo "$MA13")) else MA03=$(while read MZ1 MZ2 MZ3 MZ4; do echo "$MZ1 $MZ4 $MZ3 $MZ2"; done <<< $(echo "$MA13")) fi fi MA14=$(while read MZ1 MZ2 MZ3 MZ4; do for i in {1..4}; do read MA03$i <<< $(echo "$MA03" | cut -d " " -f $i | head -n 2 | tail -n 1); done ; echo "$(echo "scale=30; $MZ1*$MA032 - $MZ2*$MA031" | bc -l) $MZ2 $(echo "scale=30; $MZ3*$MA032 - $MZ2*$MA033" | bc -l) $(echo "scale=30; $MZ4*$MA032 - $MZ2*$MA034" | bc -l)"; done <<< $(echo "$MA03")) for i in {3..4}; do read MA14$i <<< $(echo "$MA14" | cut -d " " -f $i | head -n 3 | tail -n 1 | sed 's/-//g'); done Ss2=$(echo "($MA143 + $MA144)*100000000000000/2" | bc -l | cut -f 1 -d '.' ) if [ $Ss2 -eq 0 ]; then zenity --info --width="280" --title="Fehler" --text "Matrix\n\n ist nicht invertierbar" exit fi if [[ $(echo "100000000000000*$MA143/1" | bc) -gt $Ss2 ]]; then MA04=$(echo "$MA14") else MA04=$(while read MZ1 MZ2 MZ3 MZ4; do echo "$MZ1 $MZ2 $MZ4 $MZ3"; done <<< $(echo "$MA14")) fi MA15=$(while read MZ1 MZ2 MZ3 MZ4; do for i in {1..4}; do read MA04$i <<< $(echo "$MA04" | cut -d " " -f $i | head -n 3 | tail -n 1); done ; echo "$(echo "scale=30; $MZ1*$MA043 - $MZ3*$MA041" | bc -l) $(echo "scale=30; $MZ2*$MA043 - $MZ3*$MA042" | bc -l) $MZ3 $(echo "scale=30; $MZ4*$MA043 - $MZ3*$MA044" | bc -l)"; done <<< $(echo "$MA04")) MA154=$(echo "$MA15" | cut -d " " -f 4 | head -n 4 | tail -n 1) if [[ $(echo "100000000000000*$MA154/1" | sed 's/-//' | bc) -ne 0 ]]; then MA05=$(echo "$MA15") else zenity --info --width="280" --title="Fehler" --text "Matrix\n\n ist nicht invertierbar" exit fi MA06=$(while read MZ1 MZ2 MZ3 MZ4; do for i in {1..4}; do read MA05$i <<< $(echo "$MA05" | cut -d " " -f $i | head -n 4 | tail -n 1); done ; echo "$(echo "scale=30; $MZ1*$MA054 - $MZ4*$MA051" | bc -l) $(echo "scale=30; $MZ2*$MA054 - $MZ4*$MA052" | bc -l) $(echo "scale=30; $MZ3*$MA054 - $MZ4*$MA053" | bc -l) $MZ4"; done <<< $(echo "$MA05")) MA07=$(while read MZ1 MZ2 MZ3 MZ4; do for i in {1..4}; do read MA06$i <<< $(echo "$MA06" | cut -d " " -f $i | head -n $i | tail -n 1); done ; echo "$(echo "$MZ1/$MA061" | bc -l) $(echo "$MZ2/$MA062" | bc -l) $(echo "$MZ3/$MA063" | bc -l) $(echo "$MZ4/$MA064" | bc -l)"; done <<< $(echo "$MA06")) MA08=$(echo "$MA07" | tail -n 4 | sed 's/ /\n/g' | sed 's/^0$/0.0/' | sed -r 's/^(-?)\./\10./' | sed -r 's/(\.?)0*$//' | pr -t -s" " -4 | sed 's/ /\t/g') MA09=$(while read zeile; do if [ $(echo $zeile | grep - | wc -w) -eq 0 ]; then echo "$zeile+.000000000005" | bc -l ; else echo "$zeile-.000000000005" | bc -l ; fi; done <<< $(echo "$MA07" | tail -n 4 | sed 's/ /\n/g') | sed -r '/\./ s/.{12}$//' | sed 's/^0$/0.0/' | sed -r 's/^(-?)\./\10./' | sed -r 's/(\.?)0*$//' | pr -t -s" " -4 | sed 's/ /\t/g') zenity --text-info --title="Die inverse Matrix lautet" --width=960 --height=360 <<< $(cat <(echo "$MA08") <(echo -e "\nauf 8 Stellen nach dem Komma\n") <(echo "$MA09")) |
| Nun muß man das script ausführbar machen. |
| chmod +x ~/Bla/4x4-Matrix-invertieren.sh |
| Die Eingabe kann man auch in das zenity-Fenster hineinkopieren, wenn Kommazahlen, Punkt-Zahlen, Brüche und Multiplikationen wild durcheinander vorgegeben sind |
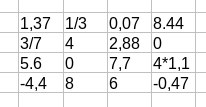
|
Nach dem Kopieren in das Eingabefenster von 4x4-Matrix-invertieren.sh erhält man die Inverse |
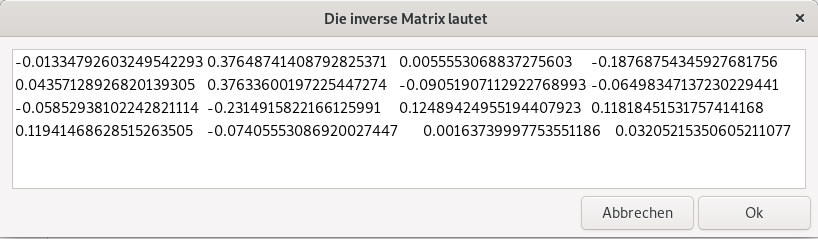
| Man kann auch eine Matrix mit Funktionsausdrücken eingeben. Natürlich muß man die Eingabe so schreiben daß bc diese versteht |

|
Man muß in diesem Fall in das zenity-Eingabefenster hineinkopieren e(l(2)/2) 4*a(1) 0 e(l(11)/3) 1 -e(l(3)/2) -4*a(1) 0 e(1) 1 e(l(5)/2) 4*a(1) e(l(e(1))/3) -e(1) 1 -e(l(7)/2) Bei mehreren Matrix-Eingabezahlen die etliche Nullen nach dem Komma besitzen, wie z.B. 0.0000000439 versagt dieses script da die Multiplikationen immer mehr Nullen nach dem Komma erzeugen und dies irgendwann zu 0 gerundet wird. Man vergleiche dazu: |
| echo .0000001515*.0000002424*.0000001616 | bc -l |
|
0 Die Info-Ausgabe daß es keine Inverse gibt ist in diesem Fall keine Wahrheits-Garantie. Man kann in diesem Fall die Inverse von 100000000*A bestimmen und das Ergebnis mit 100000000 korrigieren. Man kann das 4x4-Matrix-script auch zur Bestimmung der Inverse einer 3x3-Matrix verwenden. Dazu erweitert man das Zahlenschema in der folgenden Form: |
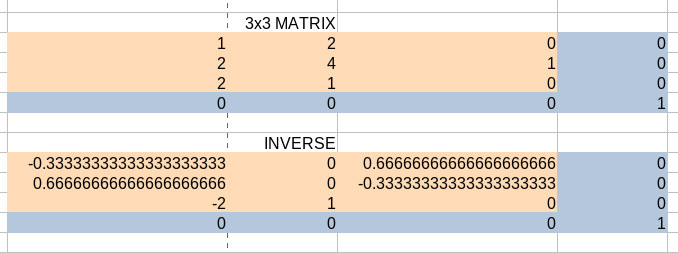
|
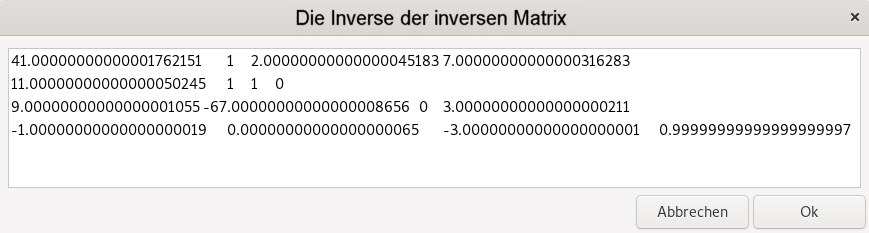
Noch eine Anmerkung zu den Rundungsfehlern. Man kann für eine Matrix mit dem script 4x4-Matrix-invertieren.sh die inverse Matrix bestimmen. Die ausgegebenen Werte kann man kopieren und wieder in das script 4x4-Matrix-invertieren.sh eingeben. Damit berechnet man die Inverse der inversen Matrix, was eigentlich die Ausgangsmatrix wieder zurückgeben soll. Bei dem ersten Beispiel auf dieser Seite ist das auch der Fall. Aber wenn die Zahlen viele Stellen nach dem Komma aufweisen werden durch die Multiplikationen doch Rundungsfehler auftreten: |

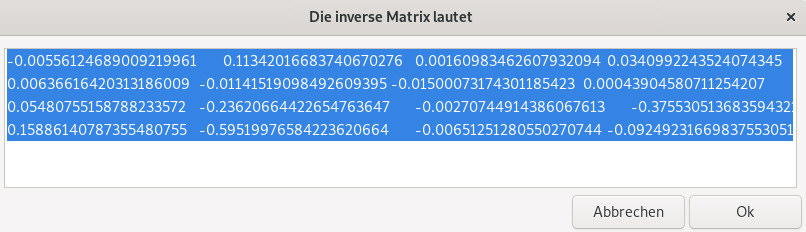
|
Diese Rundungsfehler erscheinen aber viele Stellen nach dem
Komma und die Ausgabe sollte für
brauchbare Ergebnisse ausreichen. Das script wurde daher durch eine Ausgabe mit 8 Stellen nach dem Komma erweitert. Rundungsfehler bei Computer-Berechnungen tauchen schon bei einfachen Berechnungen auf, hier ein Bruch. |
| echo "6/13666" | bc -l |
|
.00043904580711254207 Multipliziert man das Ergebnis mit dem Nenner des Bruches: |
| echo "0.00043904580711254207*13666" | bc -l |
|
5.99999999999999992862 Man hat eine Abweichung von 6, aber erst viele Stellen nach dem Komma. |
|
Ein
Beispiel aus der Chemie: Auf der Seite http://sciencesoft.at/equation/index?lang=de habe ich das folgende Beispiel gefunden. Durch Einleiten von Chlor Cl2 in heiße Kalilauge entstehen folgende Reaktionsprodukte: Kaliumchlorat, Kaliumchlorid und Wasser H2O. Kalilauge ist die wässrige Lösung von Kaliumhydroxid KOH Kaliumhydroxid wird z.B. zur Herstellung von Schmierseifen, Waschmitteln, Backofenreinigern verwendet. Kaliumchlorat KClO3 wird z.B. in Zündköpfen von Streichhölzern verwendet. Kaliumchlorid KCl wird z.B. in der Lebensmitteltechnik als Festigungsmittel und Geschmacksverstärker eingesetzt. Es stellt sich die Frage aus wievielen Teilen der Ausgangsstoffe wieviele Teile der Reaktionsprodukte entstehen. Mit x1 bis x5 für die eingesetzten Mengen bei den 5 beteiligten Produkten erhält man die Gleichung |
![]()
| Die Anzahl der Atome der Ausgangsprodukte (linke Seite) muß natürlich mit der Anzahl der Atome der Reaktionsprodukte (rechte Seite) übereinstimmen. Damit erhält man folgende Gleichungen |

|
Die Matrix A lautet also 1 0 -1 -1 1 0 -3 0 1 0 0 0 0 2 -1 -1 Mit dem script 4x4-Matrix-invertieren.sh kann man die inverse Matrix bestimmen.Diese lautet 0 0 1 0 -1/2 0 1/2 1/2 0 -1/3 1/3 0 -1 1/3 2/3 0 Das script zeigt Komma-Zahlen mit 20 Stellen nach dem Komma aber man kann schnell die entsprechenden Brüche erkennen. Wenn man unsicher ist kann man die Matrix mit den Brüchen wieder in das script 4x4-Matrix-invertieren.sh eingeben und damit die Inverse der inversen Matrix bestimmen, die mit der Matrix A übereinstimmt. Man erhält die Lösung |
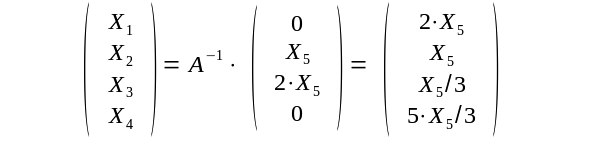
|
Die Mengen sind als Anzahl von Atomen natürlich positive ganze Zahlen. Daher ist
das Ergebnis nur sinnvoll wenn x5 durch 3 teilbar ist. Also x5 = 3 Vielfache von 3 ergibt nur Vielfaches des Gesamtprozesses. Damit ergibt sich die Reaktionsgleichung |
![]()
|
Ein anderer Reaktionsprozess von der oben angegebenen Chemie-Seite.
Es stellt sich wieder die Frage aus wievielen Teilen der Ausgangsstoffe wieviele Teile der Reaktionsprodukte entstehen. Mit x1 bis x6 für die eingesetzten Mengen |
![]()
|
Die Anzahl der Atome der Ausgangsprodukte (linke Seite) muß natürlich
mit der Anzahl der Atome der Reaktionsprodukte (rechte Seite)
übereinstimmen. Damit erhält man folgende Gleichungen Für As : 2x1 = x4 Für S: 3x1 = x5 Für H: x2 + 2x3 = 3x4 + 2x5 Für O: 3x2 + x3 = 4x4 + 4x5 + x2 Für N : x2 = x6 Die letzte Gleichung zeigt daß man die sechste Unbekannte durch die zweite ersetzen kann. |

|
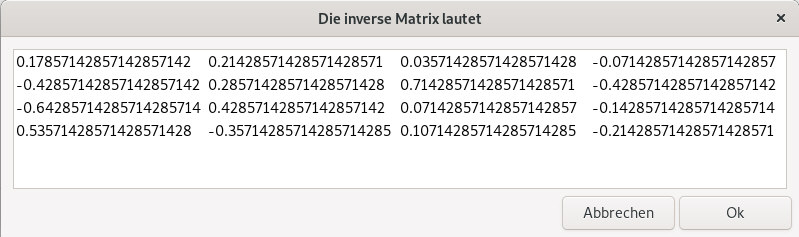
Die Matrix A lautet also 2 0 -1 0 3 0 0 -1 0 2 -3 -2 0 1 -4 -4 Mit dem script 4x4-Matrix-invertieren.sh kann man die inverse Matrix bestimmen.Diese lautet |
|
Hier lassen sich recht schlecht Brüche erkennen. Mit etwas mehr Mathematik kann man so vorgehen. Man kann benutzen |
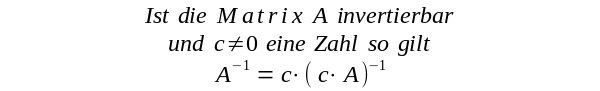
|
Dafür berechnet man die Determinante von A det A = 28 Nun berechnet man cA mit c= 1/28 2/28 0 -1/28 0 3/28 0 0 -1/28 0 2/28 -3/28 -2/28 0 1/28 -4/28 -4/28 Mit dem script 4x4-Matrix-invertieren.sh kann man von dieser Brüche-Matrix die Inverse bestimmen. Diese lautet 5 6 1 -2 -12 8 20 -12 -18 12 2 -4 15 -10 3 -6 Nun bildet man mit c = 1/28 die ursprünglich gesuchte inverse Matrix von A 5/28 6/28 1/28 -2/28 -12/28 8/28 20/28 -12/28 -18/28 12/28 2/28 -4/28 15/28 -10/28 3/28 -6/28 Man erhält die Lösung |

|
Die Mengen sind als Anzahl von Atomen natürlich positive ganze Zahlen. Daher ist
das Ergebnis nur sinnvoll wenn x2 durch 28 teilbar ist. Also x2 = 28 Vielfache von 28 ergibt nur Vielfaches des Gesamtprozesses. Damit ergibt sich die Reaktionsgleichung |
![]()
|
Ein Beispiel aus der Mathematik.
Es seien 5 Punkte in einem Koordinatensystem gegeben |
![]()
|
Nun möchte man eine Kurve durch diese Punkte legen. Diese Kurve sollte
einfach sein und einen glatten Verlauf haben. Es liegt nahe ein Polynom
4.Grades zu nehmen. f(x)=a.x4 + b.x3 + c.x2 + d.x + e Die Koeffizienten a b c d e sind so zu bestimmen daß die Kurve durch obige Punkte verläuft. Für den mittleren Punkt mit x-Wert 0 erhält man sofort -0,1=e Damit wird die Polynomgleichung a.x4 + b.x3 + c.x2 + d.x = f(x) + 0,1 Einsetzen der anderen Punktwerte ergibt 4 Gleichungen für 4 Unbekannte: |
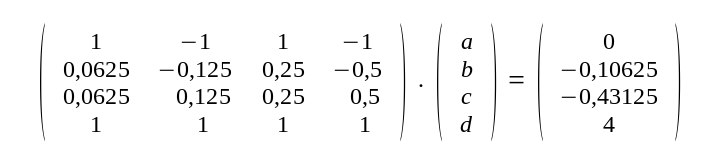
|
Die Matrix A lautet also 1 -1 1 -1 0,0625 -0,125 0,25 -0,5 0,0625 0,125 0,25 0,5 1 1 1 1 Mit dem script 4x4-Matrix-invertieren.sh kann man die inverse Matrix bestimmen.Diese lautet |

|
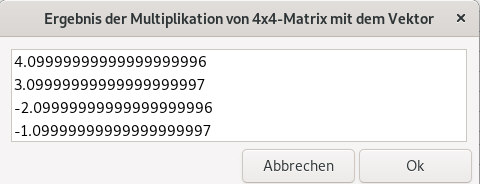
kopiert man dies bei Aufruf des scriptes 4x4-Matrix-mal-Vektor.sh ein, zusammen mit den Vektor-Werten auf der rechten Seite, so erhält man |
|
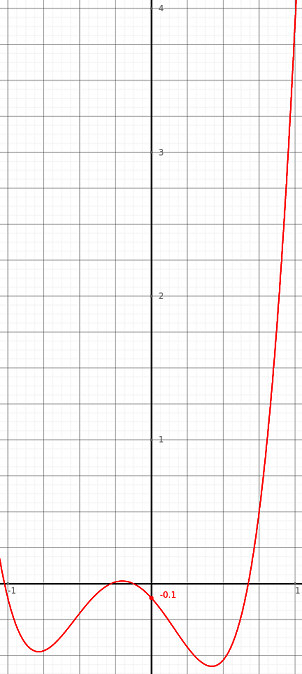
Das gesuchte Polynom lautet somit f(x)=4,1.x4 + 3,1.x3 - 2,1.x2 - 1,1.x - 0,1 |
|
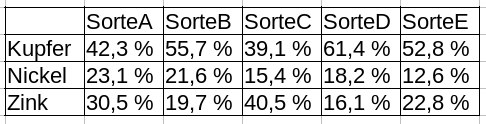
Ein Beispiel aus der Mischungsrechnung. Ein metallverarbeitender Betrieb stellt aus Neusilber die unterschiedlichsten Gebrauchsgegenstände her. Verwendungsmöglichkeiten für Neusilber kann man schnell im Internet nachschauen. Es gibt verschiedene Sorten-Posten aus Stanzabfällen, Altmetall-Sammlungen und Fehlproduktionen: |
|
Es soll eine Legierung aus 49%Kupfer, 18%Nickel und 28%Zink hergestellt
werden. Die gewünschte Menge ist 1000kg. Es bezeiche in kg a die Menge der SorteA b die Menge der SorteB c die Menge der SorteC d die Menge der SorteD e die Menge der SorteE 50% der Menge x berechnet sich durch 0,5.x Damit ergibt sich für Kupfer 0,423.a + 0,557.b + 0,391.c + 0,614.d + 0,528.e=0,49.1000 und für Nickel 0,231.a + 0,216.b + 0,154.c + 0,182.d + 0,126.e=0,18.1000 und für Zink 0,305.a + 0,197.b + 0,405.c + 0,161.d + 0,228.e=0,28.1000 Aber es gibt noch eine vierte Gleichung die zu berücksichtigen ist, nämlich daß die Addition aller Mengen gleich 1000 ist a + b + c + d + e=1000 Für die einzelnen Sorten ergibt die Addition der %-Werte von Kupfer, Nickel und Zink keine 100%. Es verbleiben Reste an anderen Elementen, und diese Reste sind auch unterschiedlich bei den verschiedenen Sorten. Damit ist die vierte Gleichung wichtig für die Berechnung. Würde die Addition der %-Werte bei jeder Sorte immer den gleichen Wert ergeben so würde sich die vierte Gleichung aus den anderen Gleichungen ergeben. Es würden keine neuen Informationen vorliegen, die vierte Gleichung wäre linear abhängig von den anderen drei. Aber dies ist hier nicht der Fall. Es ergeben sich 4 Gleichungen für 5 Unbekannte. Eine Unbekannte muß zurückgestellt werden, z.B. e |
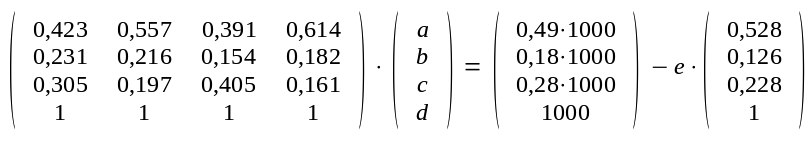
|
Die Matrix A ist links zu sehen
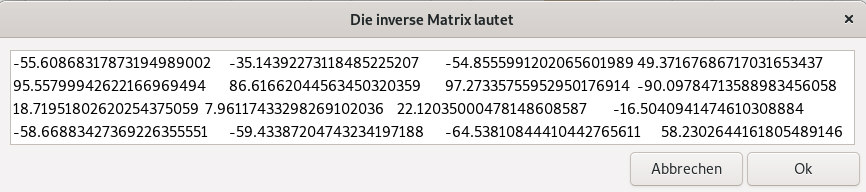
Mit dem script 4x4-Matrix-invertieren.sh kann man die inverse Matrix bestimmen. Diese lautet |
|
kopiert man dies bei Aufruf des scriptes 4x4-Matrix-mal-Vektor.sh ein, zusammen mit jeweils einem der beiden Vektoren auf der rechten Seite, so erhält man |
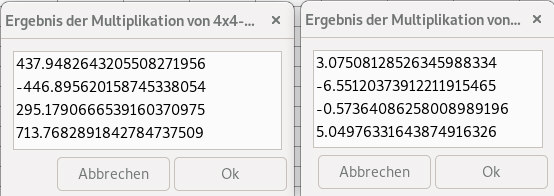
| Die Lösung somit, durch die Rundungen natürlich nur sehr gut angenähert |
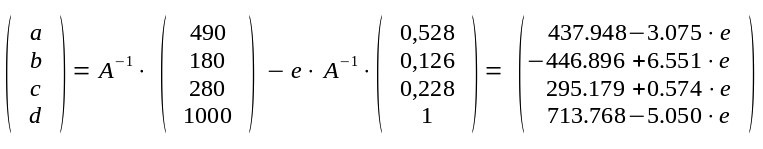
|
Es scheint beliebige Lösungen zu geben, je nach der Wahl von Menge e.
Aber man muß berücksichtigen daß die Mengen nicht negativ
werden dürfen. Die Freiheit in der Wahl für e kann für weitere Überlegungen
genutzt werden. |
|
Ein Beispiel für eine Matrix mit Funktionsausdrücken.
Im folgenden gelte für den Definitionsbereich der Funktionen: alle reellen Zahlen ohne die Nullstellen im Nenner. Stammfunktionen zu finden kann schwierig sein. Natürlich gibt es einfache Fälle |
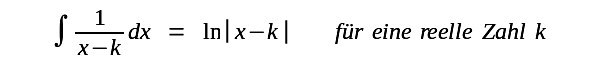
| Aber für diese Funktion |
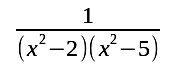
| braucht man schon ein wenig Technik. Das Polynom im Nenner hat 4 einfache Nullstellen. Dies sieht man leicht mit der 3.binomischen Formel. Die Mathematik sagt dann daß es Zahlen a b c d gibt mit |
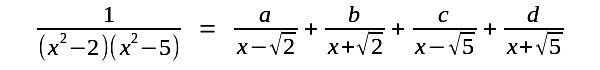
| Damit ist für diese Funktion die Stammfunktion gefunden |
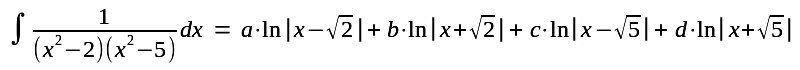
| Allerdings muß man noch die Zahlen bestimmen. Multiplikation der abcd-Gleichung mit (x2 - 2).(x2 - 5) ergibt |
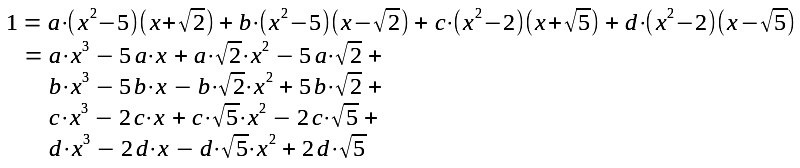
|
Dies ist eine Funktion E.x3 + F.x2 + G.x + H die für alle x stets Null ergibt und damit muß E=0 F=0 G=0 H=0 sein. Damit hat man 4 Gleichungen für 4 Unbekannte |
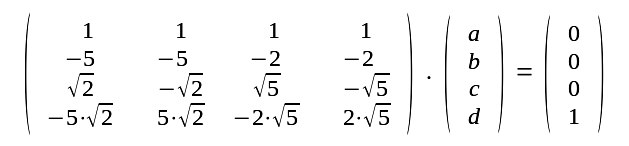
|
Die Matrix A lautet also 1 1 1 1 -5 -5 -2 -2 e(l(2)/2) -e(l(2)/2) e(l(5)/2) -e(l(5)/2) -5*e(l(2)/2) 5*e(l(2)/2) -2*e(l(5)/2) 2*e(l(5)/2) Kopiert man dies in das script 4x4-Matrix-invertieren.sh so erhält man die inverse Matrix. Diese lautet |
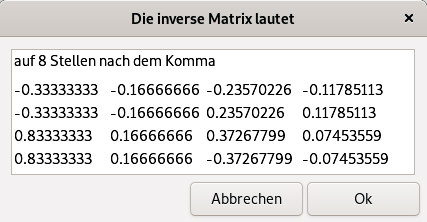
| Die Lösung somit, durch die Rundungen natürlich nur sehr gut angenähert |