|
Federpendel Stoßdämpfer Wenn ein Auto durch ein Schlagloch fährt wird der Abstand von Straße und Auto durch einen Stoß verändert. Durch die eingebaute Federung wird dieser Stoß abgefangen und das Auto in ein schwingendes System überführt. Weitere Bauteile des Autos haben die Aufgabe diese Schwingung möglichst schnell abklingen zu lassen.Daher ist es interessant sich mit schwingenden Systemen zu beschäftigen. Ein einfaches Modell ist das an einer Feder aufgehängte Gewicht. |
![]()
| Beschreiben möchte man die räumliche Veränderung des Schwerpunktes des Gewichtes. Man führt ein Koordinatensystem ein in dem die Höhe y(t) als Funktion der Zeit beschrieben wird. |
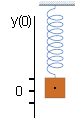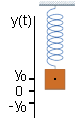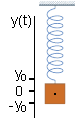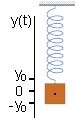
| Es wird der zeitliche Nullpunkt t=0 so gewählt daß die Auslenkung
y(0)=0 ist. Dann verändert sich die Auslenkung mit der Zeit nach oben
oder unten. Man möchte die Funktion y(t) bestimmen. Dazu wird angenommen
daß diese Funktion glatt und (mehrfach) differenzierbar ist. Dann ist
y'(t) die Geschwindigkeit und y''(t) die Beschleunigung zur jeweiligen
Zeit t. Die Kraft der schwingenden Masse m ist Masse x Beschleunigung =m.y''(t) Die Kraft der Feder ist linear der Auslenkung mit einer materialabhängigen Konstanten -D = -D.y(t) Die Kräfte müssen gleich sein und damit erhält man die Gleichung: |
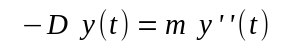
| Die Ableitung der Funktion y(t) ergibt also bis auf eine Konstante die ursprüngliche Funktion. Dieses Verhalten kennt man von der e-Funktion. Und hier ist es besonders elegant wenn man komplexe Zahlen benutzt. Insbesondere wird verwendet die komplexe Gleichung: |


| Da a eine positive reelle Zahl ist, ist sin(at) eine reelle Funktion
mit sin(0)=0 und mit wachsender Zeit zunächst monoton wachsend bis at= Dann wird der Maximalwert 1 der sinus-Funktion erreicht, d.h. die maximale y-Auslenkung y0 erreicht: y0=y( und somit ergibt sich die Lösungsfunktion. |
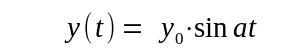
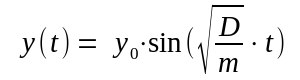
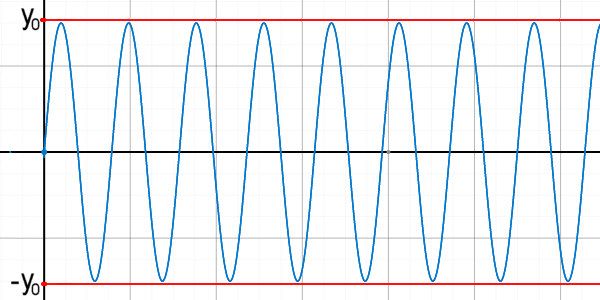
| Für die Zeit T einer Schwingungsperiode ergibt sich: |

| Die letzte Gleichung kann man nach D auflösen: |
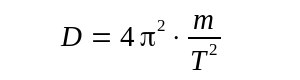
| Mit dieser Gleichung kann man durch Messung der Zeit T einer
Schwingungsperiode die Materialkonstante D der Federkraft berechnen. Stellt man das Federpendel in ein Glas Wasser, so sieht man daß die maximale Auslenkung sehr schnell abnimmt. Es liegt eine Dämpfung vor die man durch einen geschwindigkeitsabhängigen Term w.y'(t) berücksichtigen kann. Das Gleichgewicht der Kräfte wird jetzt beschrieben durch. |

| Es gibt jetzt 2 komplexe Lösungen oder 1 reelle Lösung oder 2 reelle Lösungen |

| Wählt man den zeitlichen Nullpunkt so daß die Auslenkung Null ist, y(0)=0 so folgt wieder c2=-c1 und mit einer neuen Konstanten c3=c1.2i ergibt sich die Lösung |
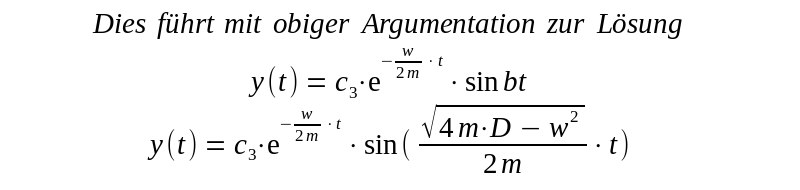
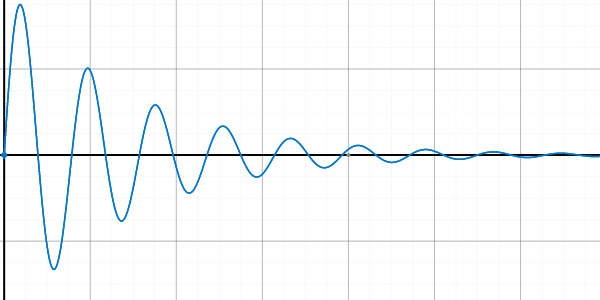
| Die neue Konstante c3 kann man nicht unmittelbar mit der
Anfangsauslenkung y0 in Verbindung bringen. Denn y0
wurde bereits gedämpft als das erste Maximum erreicht wird. Aber man
kann feststellen daß c3 eine reelle Konstante ist. Für eine konkrete Anwendung ist es aber wünschenswert wenn der zeitliche Nullpunkt so liegt, daß das erste Maximum erreicht ist. Dann hat man die maximale Stoßhöhe durch das Schlagloch vorliegen. Also y(0)= ymax y'(0)=0 Dies wird nun im nächsten Fall zugrundegelegt |
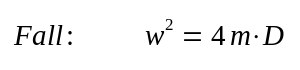
| Hier gibt es nur eine Lösung |
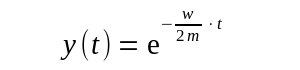
| Aber in diesem Fall gibt es eine weitere Lösung die durch den obigen Lösungs-Ansatz nicht erfaßt wurde |
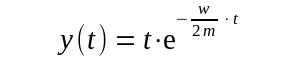
| Die allgemeine Lösung schreibt sich mit zwei Konstanten |
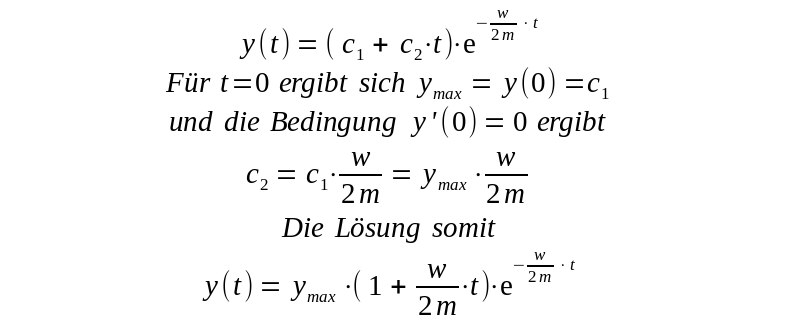
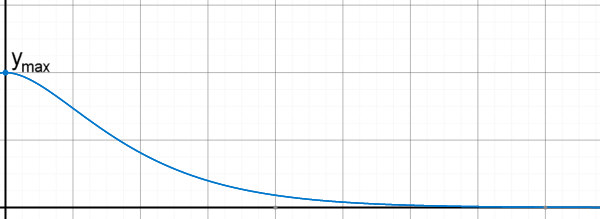
| Bei dem Fall der 2 reellen Lösungen für B fehlen die schwingenden
Teile die durch imaginäre Zahlen ausgelöst werden. Man hat hier eine
Dämpfung ähnlich dem Fall w2=4mD Allerdings ist das Abklingen langsamer. Daher ist die entscheidende Bedingung für eine schnelle Dämpfung w2=4mD Diese schnelle Dämpfung ist nicht nur bei einem Stoßdämpfer von Autos oder Motorrädern wichtig. Auch Zeiger von analogen Meßgeräten, Resonanzkörper von Musikinstrumenten, das Ausschwingverhalten eines RCL- Kreises bei elektronischen Bauteilen und vieles mehr sind Anwendungen. |