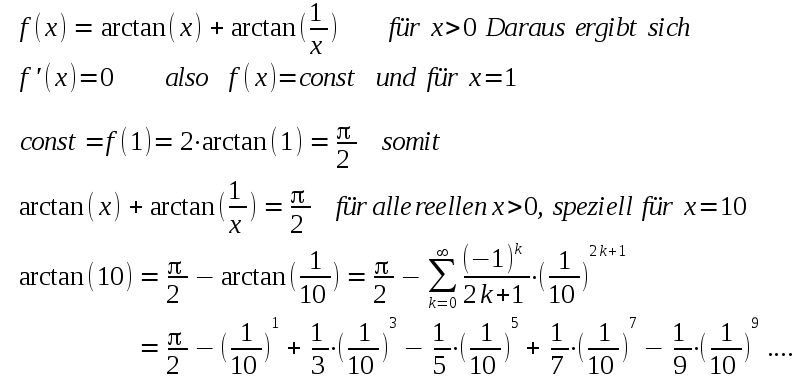Mathematik Grenzwerte

Grenzwerte

Die reellen Zahlen lassen sich der Größe nach anordnen. Man kann also sagen daß eine Zahl größer oder kleiner als eine andere Zahl ist. Dies ist bei komplexen Zahlen nicht möglich. Bei reellen Zahlen kann man leicht einen Abstand bestimmen und sagen daß zwei Zahlen nahe beieinander liegen, z.B.
1/3 und 0,33
liegen nahe beieinander. Man kann eine Zahlenfolge mit durchnummerierten Folgen-Elementen aufschreiben:

Je höher die natürliche Zahl n ist umso näher liegt das Folgen-Element
F_n an 1/3
Bei

(die natürliche Zahl n wächst über alle Grenzen)
werden die Folgen-Elemente die Zahl 1/3 beliebig genau berechnen. Man sagt dazu 1/3 ist der Grenzwert der Folge F_n
und schreibt.

Die einfachste Zahlenfolge ist jene deren Folgen-Elemente immer die gleiche Zahl ist, z.B.

Da alle Folgen-Elemente immer den gleichen Wert haben gilt dies auch bei

Interessanter ist es wenn sich Zahlenfolgen an einen Wert anpirschen, diese also einen Grenzwert haben der nicht mit einem Folgen-Element übereinstimmt. Z.B.

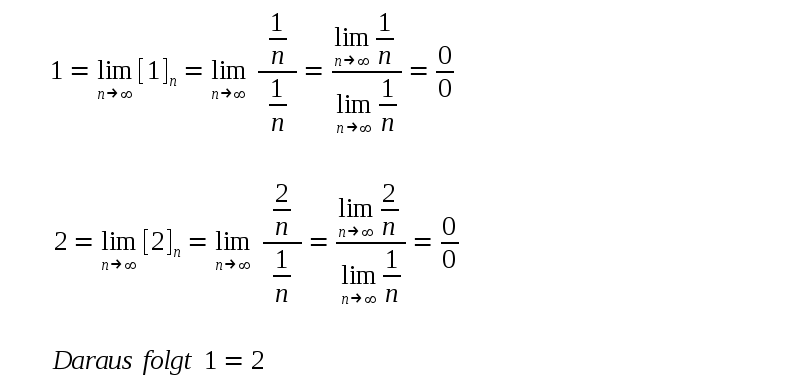
Hier ist natürlich ein Fehler gemacht worden. Sicherlich darf man nicht durch 0 teilen. Aber der wesentliche Fehler ist daß die Regeln für die lim-Bildung nicht beachtet wurden. Hier einige Regeln:

Wenn also lim im Nenner existiert und 0 ist darf man den lim nicht unter den Bruchstrich ziehen. Ein Ausdruck der Form 0/0 (oder Zahl/0 ) darf es nicht geben. Wenn irgendwo =0/0 steht so hat das die Bedeutung daß der Grenzwert beim Zähler und Nenner existiert und beidesmal 0 ist aber eine Gleichheit im Sinne von a=b existiert nicht und die Verwendung von = in diesem Zusammenhang ist irreführend und nicht vorteilhaft.

Nun ein Beispiel unter Berücksichtigung der Regeln:

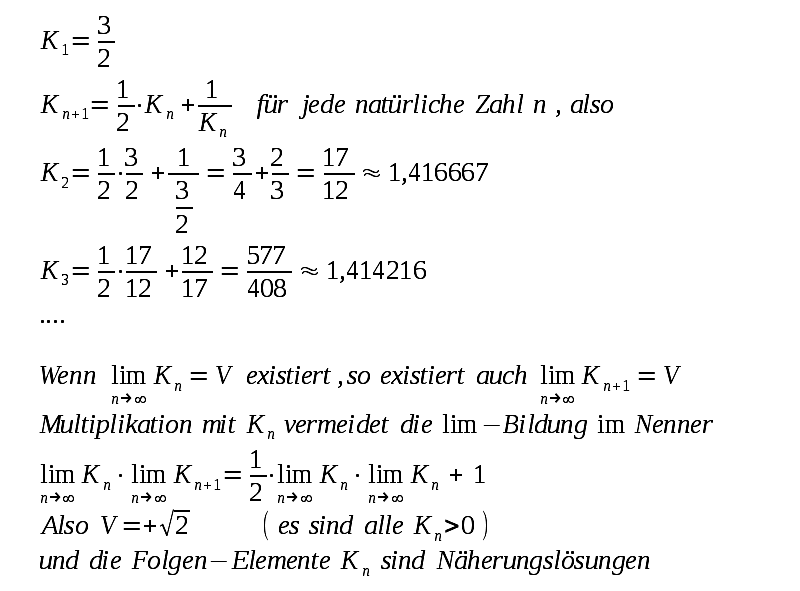
Noch zwei weitere Folgen ( L_n ist nach Wikipedia als babylonisches Wurzelziehen schon ca. 1750 v.Chr. bekannt):

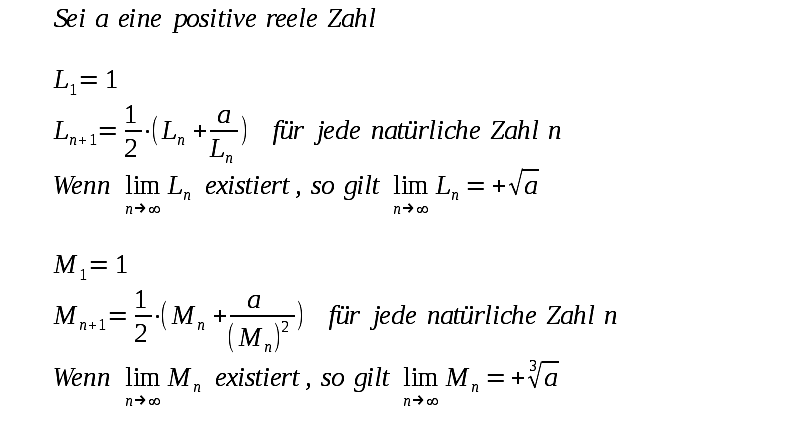
Zum Nachweis daß für eine Folge A_n ein Grenzwert existiert benutzt man oft die Regel (fallende Folge mit unterer Grenze):
Gibt es eine reelle Zahl so daß alle (evtl. bis auf endlich viele Ausnahmen) Folgen-Elemente GRÖSSER (oder gleich) sind als diese Zahl und gilt A_n+1 ≤ A_n für alle (evtl. bis auf endlich viele Ausnahmen) Folgen-Elemente, so existiert für diese Folge ein Grenzwert.

Es soll jetzt für die Folge L_n gezeigt werden daß ein Grenzwert existiert:

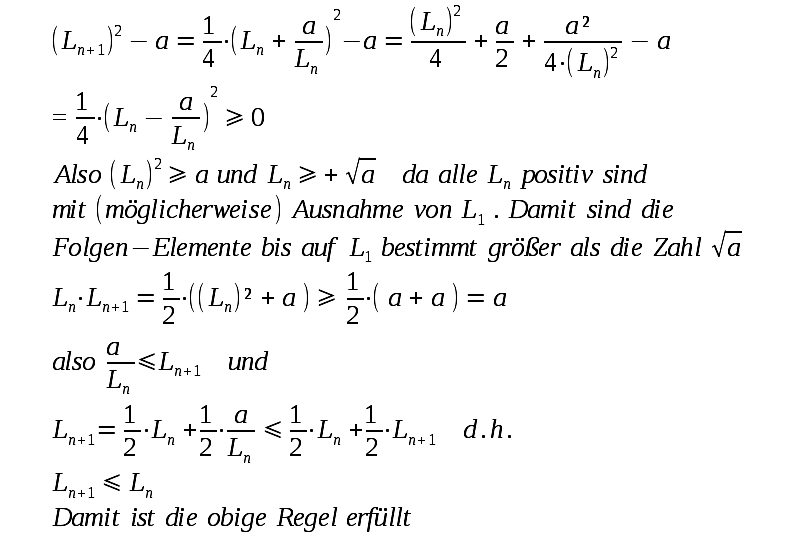
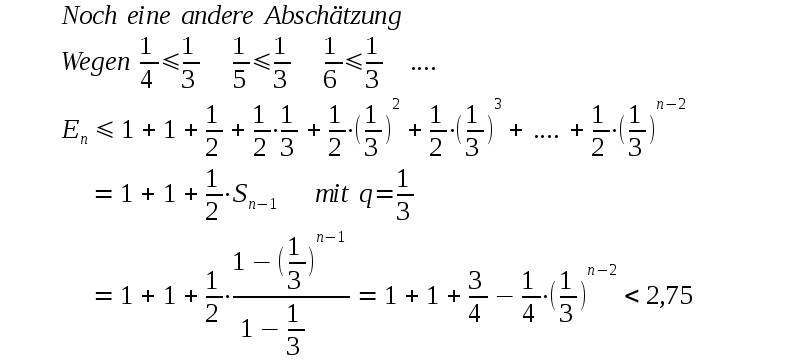
Eine sehr bekannte Folge ist

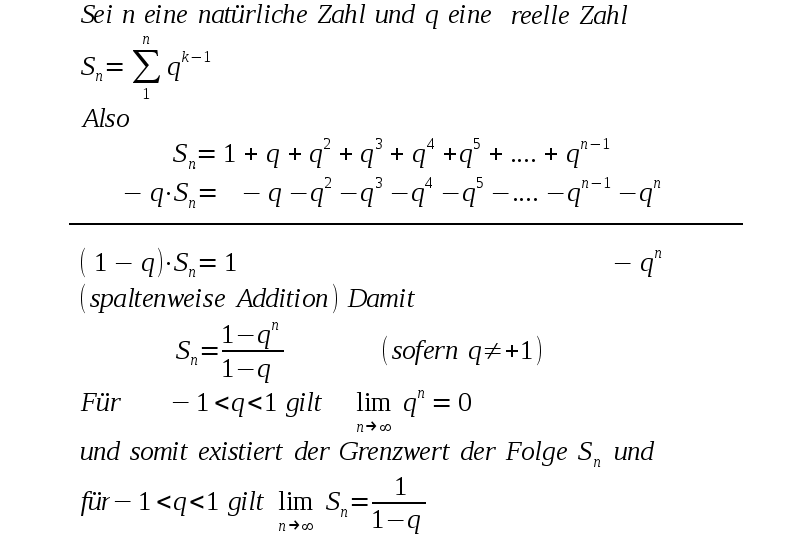
Es gibt Folgen die gegen

laufen, z.B.

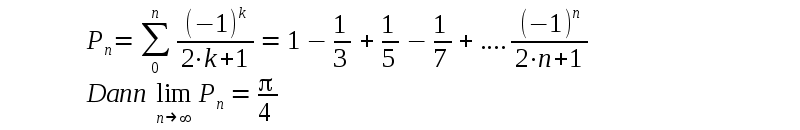
Es gibt auch Folgen über die sich "neue" Zahlen definieren, z.B. die Zahl e.

Zum Nachweis daß folgender Grenzwert existiert wird eine Regel benutzt, die analog der weiter oben verwendeten Regel funktioniert (wachsende Folge mit oberer Grenze):
Gibt es eine reelle Zahl so daß alle (evtl. bis auf endlich viele Ausnahmen) Folgen-Elemente KLEINER (oder gleich) sind als diese Zahl und gilt A_n+1 ≥ A_n für alle (evtl. bis auf endlich viele Ausnahmen) Folgen-Elemente, so existiert für diese Folge ein Grenzwert.

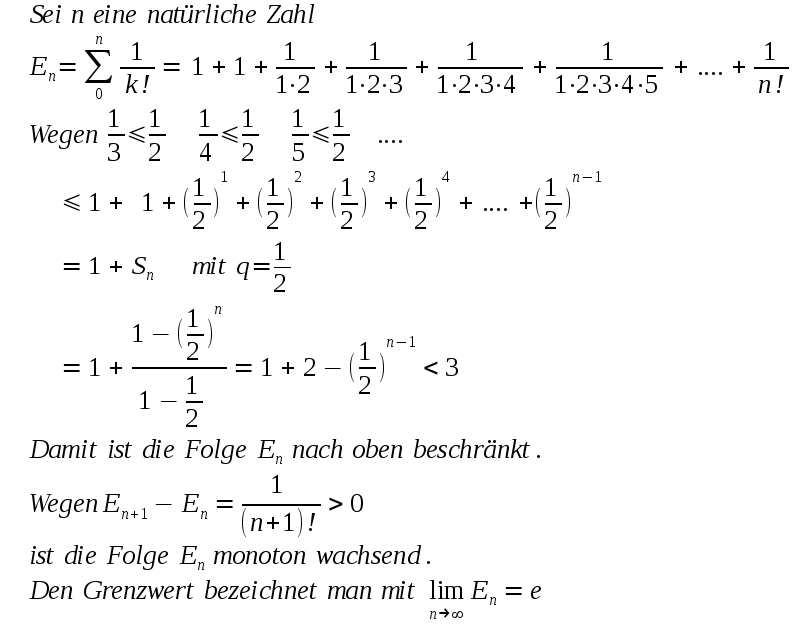
Man kann sich die Funktion f(x)=e^x anschauen

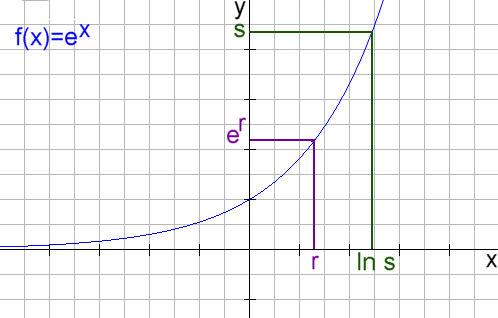
Es gibt für jede reelle Zahl r einen entsprechenden eindeutigen Funktionswert. Nimmt man eine positive reelle Zahl s auf der y-Achse so gibt es umgekehrt auch eine eindeutig bestimmte Zahl auf der x-Achse - die man den Logarithmus von s nennt und man schreibt ln(s) oder ln s.
Wählt man s=e^r so wird r=ln s

Es kann vorkommen daß für eine Folge A_n mit

auch die Folgen-Elemente selbst gegen ∞ laufen (über alle Grenzen wachsen). Einfache Beispiele sind
die Folge der natürlichen Zahlen D_n selbst oder
die Folge der geraden natürlichen Zahlen G_n

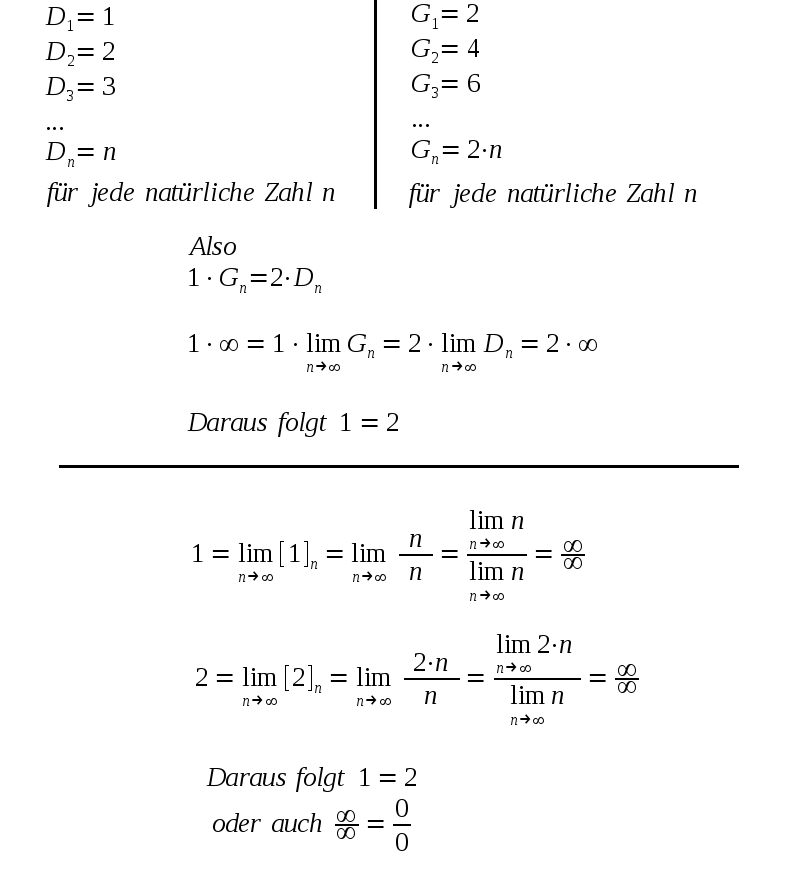
Hier sind natürlich wieder die Regeln für die lim-Bildung nicht beachtet worden.
Die lim-Bildung ist nur möglich wenn ein Grenzwert existiert. Hat die Folge aber nach oben oder nach unten keine Grenze (liegen also die Folgen-Elemente nicht ALLE zwischen zwei festen Zahlen), so gibt es keinen Grenzwert - es existiert kein lim.

Wenn irgendwo =∞ steht so hat das die Bedeutung daß kein Grenzwert existiert und die Folge über alle Grenzen wächst, aber eine Gleichheit im Sinne von a=b existiert nicht und die Verwendung von = in diesem Zusammenhang ist irreführend und nicht vorteilhaft.

Entscheidend ist immer ob ein Grenzwert für eine Folge existiert. Dann sind die Folgen-Elemente Näherungslösungen für den Grenzwert. Da ein Computer oder Taschenrechner immer nur addieren (subtrahieren) kann, und damit auch multiplizieren (dividieren) kann, werden Funktionswerte durch Näherungslösungen bestimmt. Wichtig ist dann die Anzahl der Rechenschritte, also wie schnell sich die Folgen-Elemente dem Grenzwert annähern.

Zum Bestimmen des Grenzwertes für obige Folge P_n wird etwas über die Umkehrfunktion von tan angemerkt:

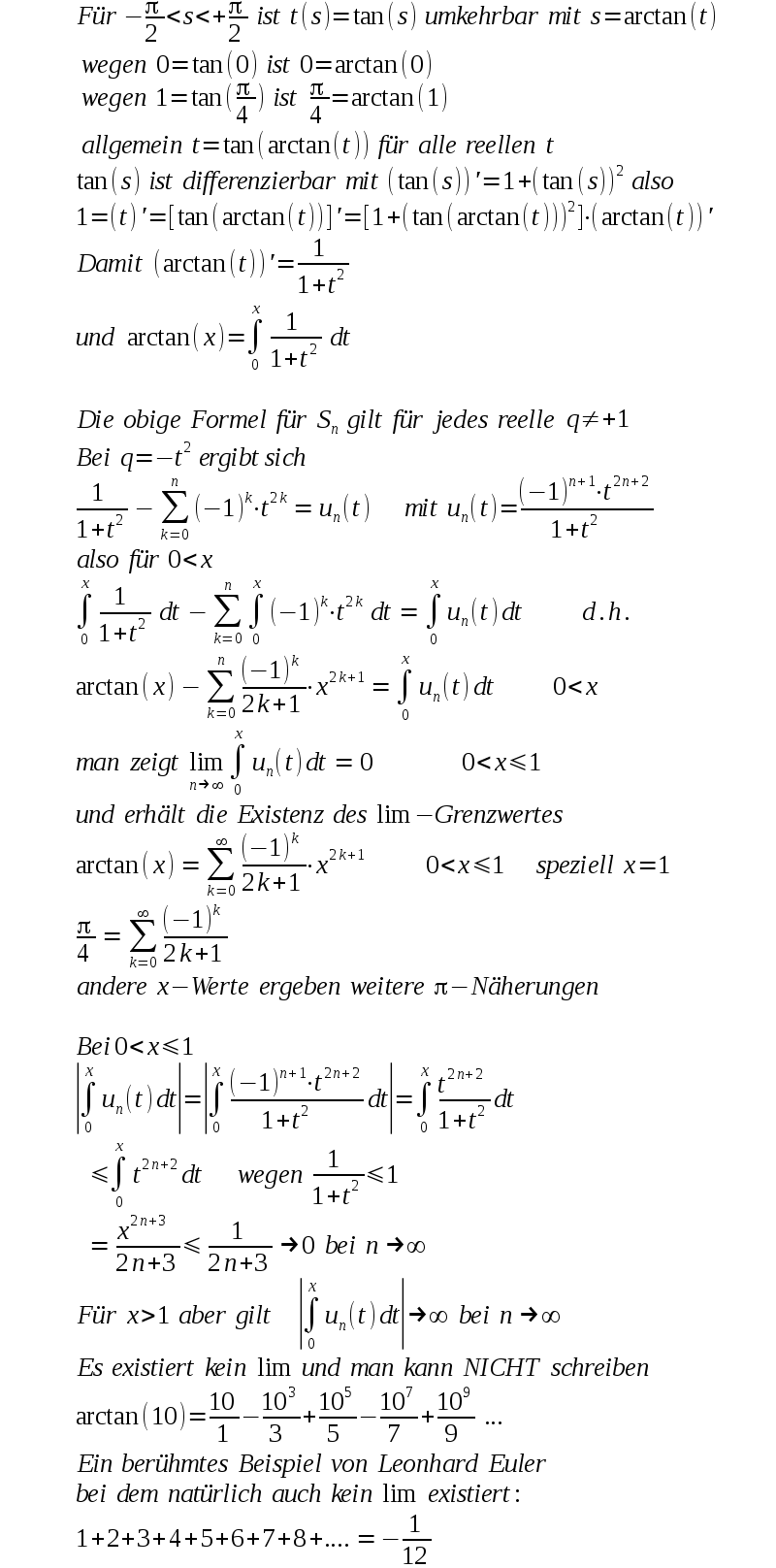
Auch für den Logarithmus kann man auf diese Art Näherungen bestimmen

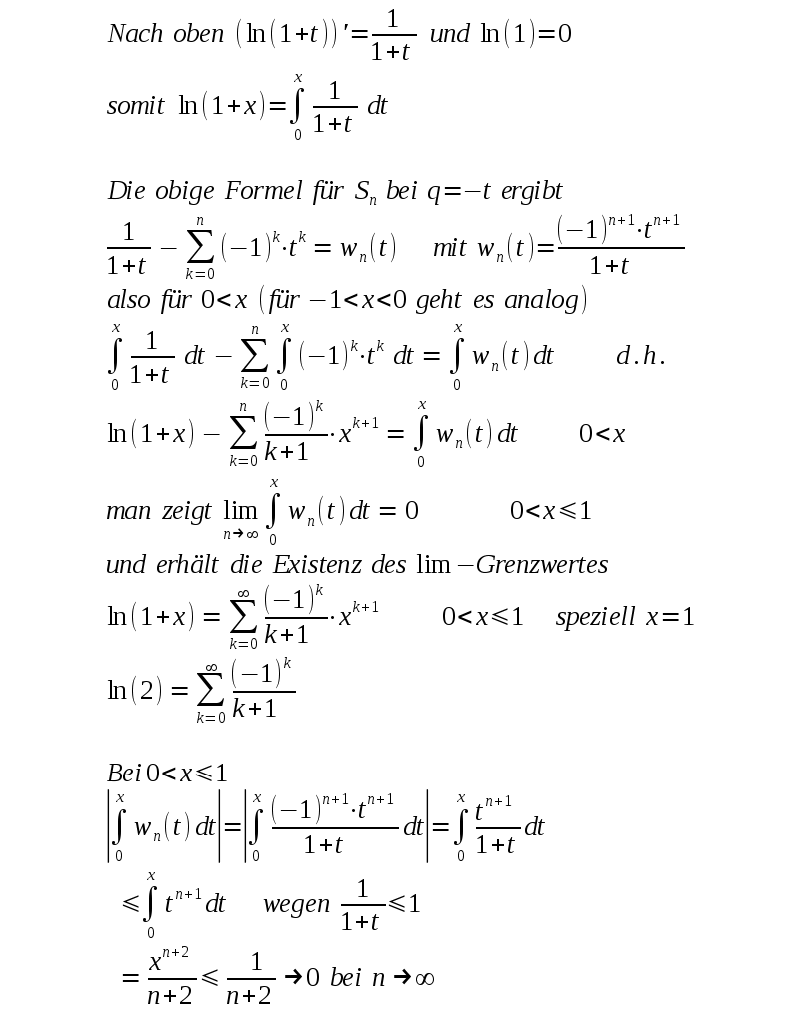
Nachdem verschiedene Möglichkeiten der Annäherung beschrieben wurden soll nun alles auf Anfang gesetzt werden. Wie beginnt man mit der Konstruktion (Definition) der Funktion f(x)=e^x ? Wie berechnet man Funktionswerte? Wie kommt man zu dem Bild mit dem Kurvenverlauf? Die Zahl e selbst ist durch eine programmierbare Vorschrift definiert worden. Computer und Taschenrechner können schnell e bis zu einer großen Annäherung berechnen. Bei 3 Stellen nach dem Komma hat man e=2,718 .

Und dies genügt schon um ein Bild der Kurve von f(x)=e^x zu zeichnen. Mit der programmierbaren Vorschrift M_n kann man 1/3-tel Werte berechnen und mit weiteren programmierbaren Vorschriften kann man beliebige Wurzeln berechnen und also im Prinzip die f(x)=e^x für jede rationale Zahl berechnen, also beliebig genau annähern. Trotzdem wäre es wünschenswert wenn es nur eine programmierbare Vorschrift zum Berechnen geben würde. Und daher startet man die Funktion f(x)=e^xmit einer Definition (die auch für komplexe Zahlen funktioniert):

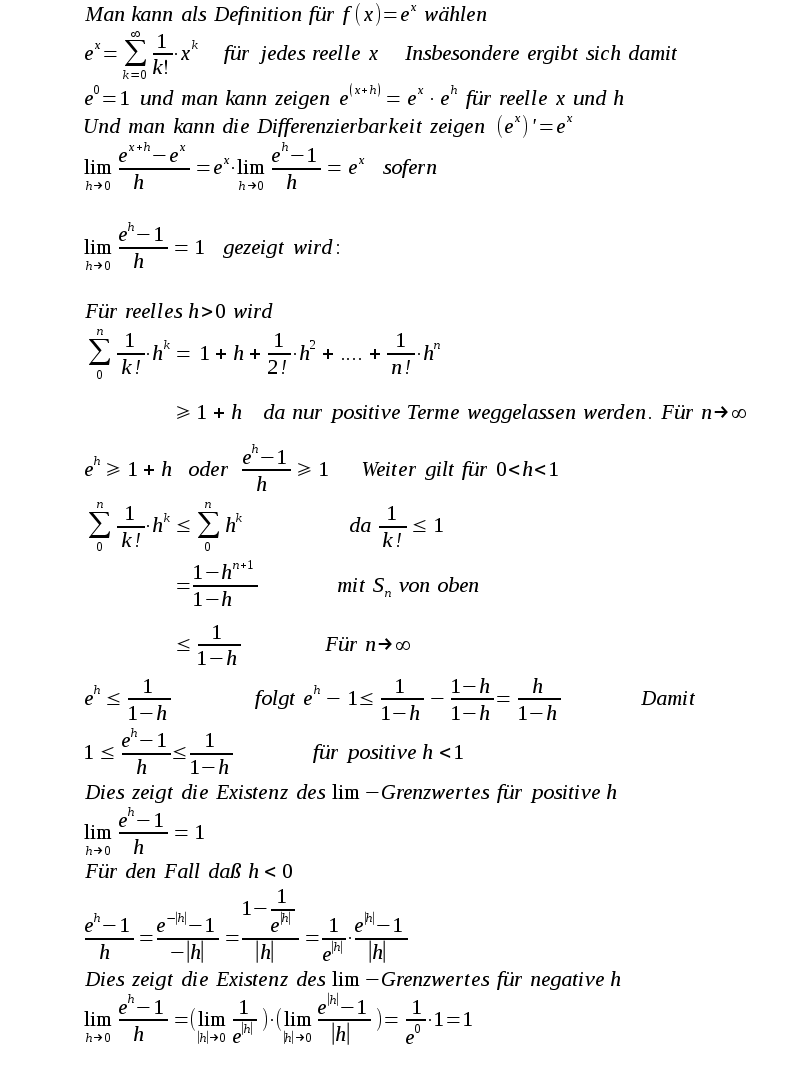
Nun noch eine Möglichkeit arctan(10) korrekt zu berechnen, also anzunähern.
Dazu betrachte man die Funktion