Mathematik Funktionen

Funktionen

Man kann auf einem Blatt Papier einen Lageplan zeichnen. Mathematisch gesehen kann man dies als ein zweidimensionales Koordinatensystem betrachten mit einem Nullpunkt im Mittelpunkt (aktueller Standort auf dem Lageplan) und x-Werten in waagrechter Anordnung und y-Werten in senkrechter Anordnung.
x-Werte: positive reelle Zahlen nach rechts (nach Osten) angeordnet,
x-Werte: negative reelle Zahlen nach links (nach Westen) angeordnet,
y-Werte: positive reelle Zahlen nach oben (nach Norden) angeordnet,
y-Werte: negative reelle Zahlen nach unten (nach Süden) angeordnet,
Jeden Punkt im Koordinatensystem kann man in der Form (x,y) eindeutig beschreiben. Stehen die x-Werte mit den y-Werten in einer Beziehung so kann man dies oft als Kurve im Koordinatensystem einzeichnen. Bsp.:

Kurve=Menge aller Punkte (x,y) für die gilt y=x

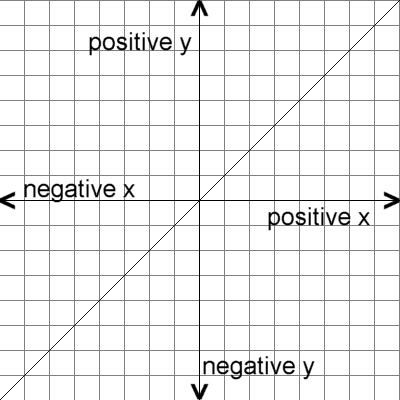
Diese spezielle Kurve nennt man oft die erste Winkelhalbierende. Andere Kurven wurden auf vorhergehenden Seiten schon gezeigt. Z.B.:

Ein Kreis mit Radius r
Kurve=Menge aller Punkte (x,y) für die gilt x²+y²=r²

Normalparabel
Kurve=Menge aller Punkte (x,y) für die gilt y=x²

Man kann in der Beziehung zwischen x und y auch x und y miteinander vertauschen und erhält eine Umkehr-Kurve. Z.B.:

Wurzel=Umkehr-Normalparabel
Umkehr-Kurve=Menge aller Punkte (x,y) für die gilt x=y²

Geometrisch erhält man die Umkehr-Kurve als Spiegelung an der ersten Winkelhalbierenden:

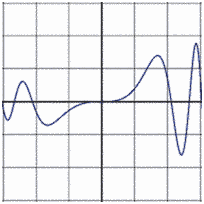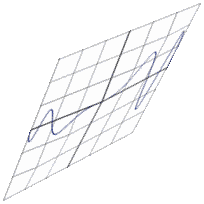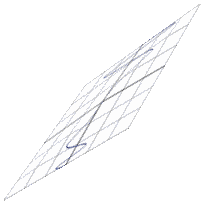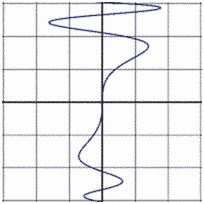
Anfangs hat man gesagt daß die Kurve von einer Funktion erzeugt wird und die Umkehr-Kurve von der entsprechenden Umkehr-Funktion. Heute bezeichnet man eine Beziehung zwischen x und y nur noch dann als Funktion wenn zu einem vorgegebenen x nur ein einziges y die Beziehung erfüllt. Man muß also die Wurzel-Kurve in zwei Funktionen zerlegen, die posive-wertige Wurzel-Funktion und die negativ-wertige Wurzel-Funktion.

Man kann sagen daß die Umkehr-Normalparabel-Kurve (die Wurzel-Kurve) zu einem vorgegebenen positiven x zwei Lösungen für y besitzt.
Heute sagt man: Die Normalparabel-Funktion läßt sich in zwei umkehrbare Funktionen zerlegen, die beide zu einem vorgegebenen positiven x jeweils eine Lösung für y besitzen.

Man kann sagen daß die Umkehr-Sinus-Kurve zu einem vorgegebenen x (-1<x<+1) unendlich viele Lösungen für y besitzt.
Heute sagt man: Die Sinus-Funktion läßt sich in unendlich viele umkehrbare Funktionen zerlegen, von denen unendlich viele zu einem vorgegebenen x (-1<x<+1) jeweils eine Lösung für y besitzen. Wählt man für die umkehrbaren Funktionen ein x-Intervall z.B. mit der Länge

/10 so gibt es auch unendlich viele umkehrbare Funktionen ohne eine Lösung.

Generell also: Die Beziehung zwischen x und y als Kurve verdeutlichen, dann in Scheibchen-Funktionen zerlegen (z.B. den Kreis in positive Kreishälfte und negative Kreishälfte) und die Scheibchen-Funktionen in weitere Scheibchen-Funktionen zerlegen, die umkehrbar sind (z.B. rechtes positives Kreisviertel, linkes positives Kreisviertel,...).
Für die obige Funktion ist hier die Scheibchen-Zerlegung farbig dargestellt:

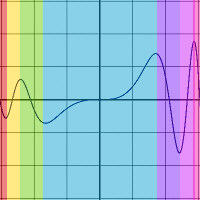
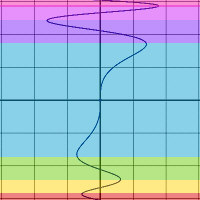
Innerhalb jedes Farbbereiches ist die Beziehung zwischen x und y umkehrbar eindeutig. Deshalb wird bei jeder Funktion neben der Beziehung zwischen x und y auch immer der Bereich angegeben in dem sich die x-Werte befinden (Definitionsbereich) und auch in welchem Bereich sich die y-Werte befinden (Wertebereich).
Oftmals müssen die Funktionen nicht umkehrbar sein. Bei Anwendungen ist es in der Regel so daß zu einem x-Wert (z.B. einem Zeitwert) nur ein y-Wert (z.B. ein Temperaturwert) gemessen werden kann. Dann gibt es eine Temperaturkurve über der Zeit, die sich schön in einem zweidimensionalen Koordinatensystem darstellen läßt und die ständig Höhen und Tiefen aufweist, so wie die Funktion zur obigen Kurve.
Will man aber einem dreidimensionalen Punkt zu einer gegebenen Zeit einen Temperaturwert zuordnen, so hat man eine Beziehung von (x,y,z,t) zu T - also einem vierdimensionalen Raumzeitpunkt zu einem Temperaturwert - was sich in einem zweidimensionalen Koordinatensystem so nicht darstellen läßt.
Solange die Beziehung zwischen reellen x und reellen y so besteht daß zu einem x nur ein bestimmtes y möglich ist, so sagt man daß y=f(x) eine reelle Funktion von x ist. Trotzdem ist es auch für reelle Funktionen äußerst vorteilhaft wenn man komplexe Zahlen berücksichtigt. Komplexe Zahlen lassen sich in der komplexen Ebene beschreiben durch einen Abstand vom Nullpunkt und einem Winkel. Aber wie genau bestimmt man diesen Winkel:

Bei der Multiplikation zweier komplexer Zahlen addieren sich die Winkel. Und mit dieser Überlegung lassen sich auf einfache Art erstaunliche Ergebnisse erzielen:

Mit diesen arctan-Reihenentwicklungen ist es also ebenfalls möglich

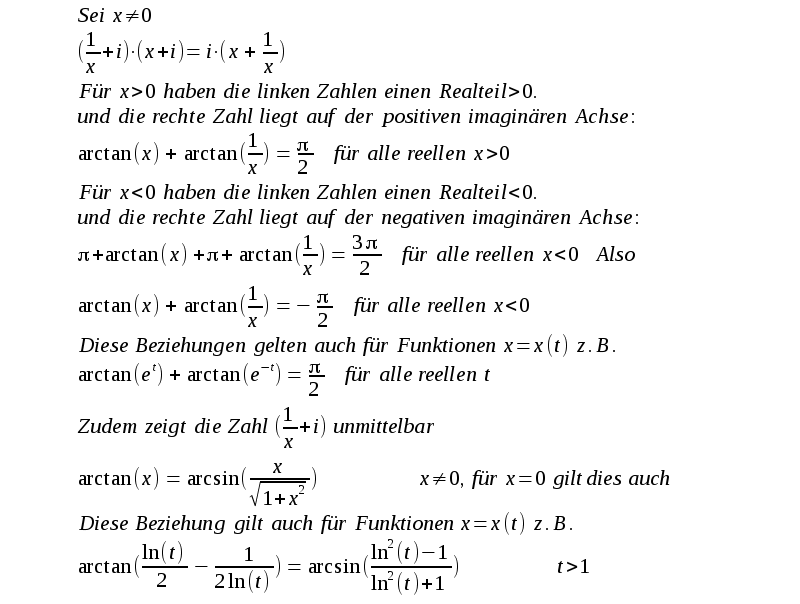
anzunähern. Die Berechnungen für eine vorgegebene Genauigkeit erfordern hier deutlich weniger Rechenoperationen als bei

=4arctan(1)

Nun noch eine falsche Argumentation:

In der Schule wird manchmal für den Winkel einer komplexen Zahl
das 2

-Intervall
[0,2

[
zugrundegelegt und mit geometrischen Überlegungen der Winkel bestimmt. Dann muß man zur Bestimmung des
Schulwinkel(1-i)
überlegen: Für welches ganzzahlige k liegt
-

/4 +2k

innerhalb des Intervalles [0,2

[
Dies ist der Fall für k=1. Also
Schulwinkel(1-i)=-

/4 + 2

= 7

/4

Und noch eine falsche Argumentation:

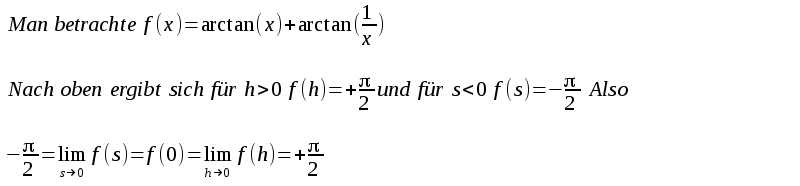
Der erste Fehler ist daß der Definitionsbereich der Funktion nicht konkret angegeben wurde. Da man nicht durch 0 teilen darf gibt es kein f(0). Eine Lösung besteht darin daß man passende Definitionsbereiche wählt und f in zwei Funktionen zerlegt:

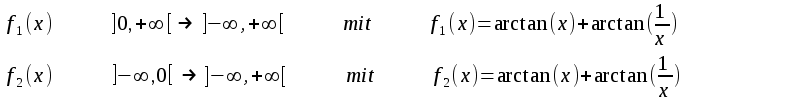
Eine andere Lösung besteht darin daß man f(0) definiert. Man hat dabei künstlerische Freiheit, meist wird der Mittelwert genommen f(0):=0 . Damit besteht der Definitionsbereich aus allen reellen x. Der zweite Fehler besteht darin zu glauben, daß der rechtsseitige lim und der liksseitige lim immer übereinstimmen. Dies ist hier nicht der Fall und es besteht auch keine Übereinstimmung mit f(0). Die Kurve der Funktion f hat einen Sprung. Die Kurvenpunkte setzen sich nicht stetig fort - man kann sie nicht zeichnen ohne den Stift vom Papier wegzunehmen und neu aufzusetzen.
Die Stetigkeit einer Funktion ist eine Eigenschaft die nicht durch ein spezielles t und ein spezielles f(t) beschrieben werden kann sondern die eine kleine Umgebung von t und eine (kleine) Umgebung von f(t) erfordert:
Sei also q eine kleine positive Zahl und x aus der Umgebung [t-q,t+q] , dann muß f(x) immer definiert sein und
für x

t muß folgen f(x)

f(t) egal aus welcher Richtung die x-Annäherung an t erfolgt.

Eine Funktion ist nicht allein eine Zuordnung von x zu y, sondern sie ist ein abstraktes Element mit Eigenschaften wie Stetigkeit, Monotonie, Differenzierbarkeit, Integrierbarkeit.