Mathematik Dirac Delta Funktion Distribution Distributionen

Distributionen

Zunächst eine Anmerkung zum Begriff der Funktion.

Eine Funktion f ist eine Vorschrift die bestimmten x-Werten (Definitionsbereich) y-Werte (Wertebereich) zuordnet.

f(x) ist die Zahl die von der Funktion dem Wert x zugeordnet wird, also ein ganz bestimmter Zahlenwert.

Eine Funktion kann monoton wachsend sein, ein Maximum haben, differenzierbar sein, umkehrbar sein, ....
Ein bestimmter Funktionswert f(x) ist lediglich eine Zahl und diese Zahl ist nicht differenzierbar, nicht stetig, nicht monoton,.... Also müßte man zunächst Funktionen definieren.

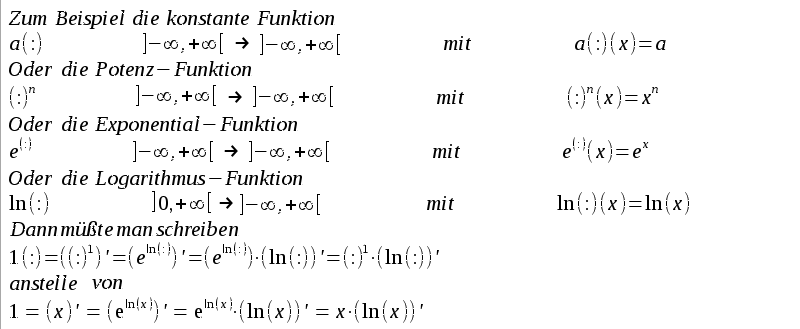
Diese Funktionen-Schreibweise ist unübersichtlich und so bleibt man lieber bei der unteren Schreibweise und behält im Kopf daß Funktionen f gemeint sind - schließlich weiß man daß Funktionswerte f(x) als Zahlenwerte nicht differenziert werden können.

Man kann sich besonders schöne Funktionen anschauen. Solche die
∞   unendlich oft differenzierbar sind,
k    die außerhalb eines endlichen Intervalles (a,b) überall 0 sind,
+   die überall nichtnegativ sind und
1    die den Flächeninhalt 1 haben:

Anschaulich ist es einleuchtend daß es solche Funktionen gibt. Aber in der Mathematik braucht man konkrete Beispiele:

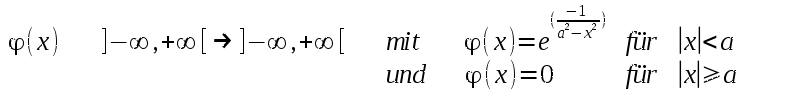
Man kann nachprüfen daß diese Funktion außerhalb des Intervalles (-a,+a) immer 0 und überall nichtnegativ ist (per Definition), daß diese Funktion unendlich oft differenzierbar ist und einen Flächeninhalt besitzt. Multipliziert man diese Funktion mit dem Faktor
1/Flächeninhalt
so hat man eine Beispiel-Funktion aus

Leichte Änderungen zeigen, daß es Beispiel-Funktionen gibt die an der Stelle 0 den Wert 0 haben und zwar für jedes noch so kleine Intervall. Oder solche die an der Stelle 0 einen beliebigen anderen Zahlenwert haben und zwar den gleichen Zahlenwert für jedes noch so kleine Intervall. Bei anderen Beispiel-Funktionen

(x) gilt für x

0 daß

(x)

∞ läuft.
Natürlich kann man diese Funktionen in ein beliebiges Intervall (a,b) verschieben. Man nennt diese Funktionen auch Testfunktionen.

Verkleinert man das Intervall (-a,+a) immer mehr, a

0 , so erhält man anschaulich eine "Funktion" die überall 0 ist mit Ausnahme der Stelle 0 und für die der Flächeninhalt 1 ist, da der Flächeninhalt jeder Funktion aus

immer 1 ist. In der Physik nennt man diese "Funktion" die Dirac-Delta-Funktion

(x). Andererseits ist die Dirac-Delta-Funktion außerhalb eines einzigen Punktes immer 0 und damit eine Annäherung an die Funktion die generell überall 0 ist und die folglich den Flächeninhalt 0 hat.
Wieder einmal hat man den "Beweis" daß 1=0 ist ?
Man kann sogar noch weiter gehen und spekulieren, daß es auf dem Intervall (-a,+a) auch Testfunktionen aus

gibt die an der Stelle x=0 für jedes Intervall immer den Wert 7 oder den Wert 0 (oder jede beliebige positive Zahl) haben und folglich gilt

(0)=7=0=jede beliebige positive Zahl oder

∞.

Die Problematik ist es den Begriff einer Funktion zu überprüfen und zu sagen was der Abstand zweier Funktionen sein soll, damit man davon sprechen kann daß sich Funktionen einander annähern. Dazu kann man sich zunächst an den Mittelwertsatz für stetige Funktionen erinnern:

Gibt man einen x-Wert A vor so kann man für v>0 Intervalle (A-v,A+v) betrachten die in der folgenden Grafik grün markiert sind.
Dann wählt man Testfunktionen die außerhalb dieser Intervalle 0 sind. Diese sind in der folgenden Grafik rechts symbolisiert.
Dann existieren Zwischenwerte im Intervall [A-v,A+v] so daß die Berechnung mit der Testfunktion nahe an dem Funktionswert f(A) liegen. Der Bereich in dem sich die angenäherten Werte bewegen wurde rot markiert. Beispiele für berechnete angenäherte Funktionswerte wurden durch rote Kreuze markiert.

Für v

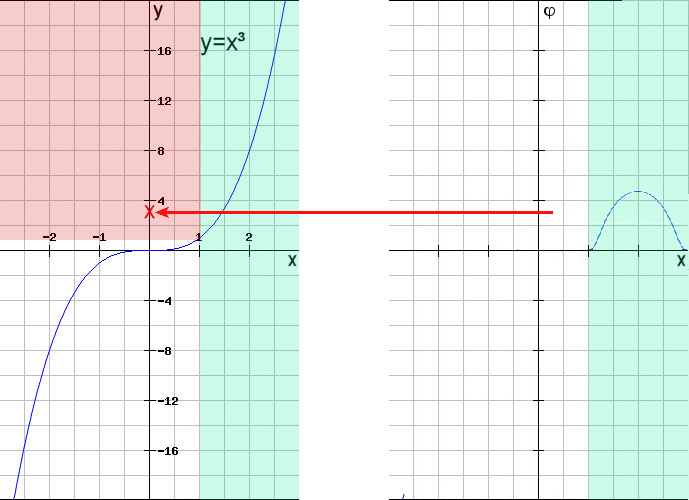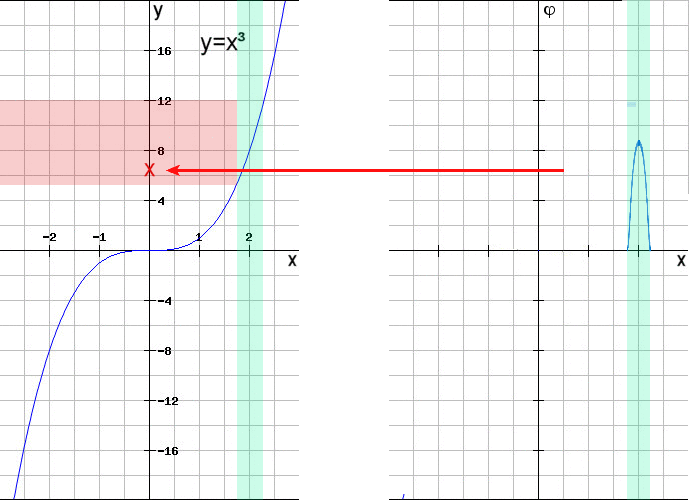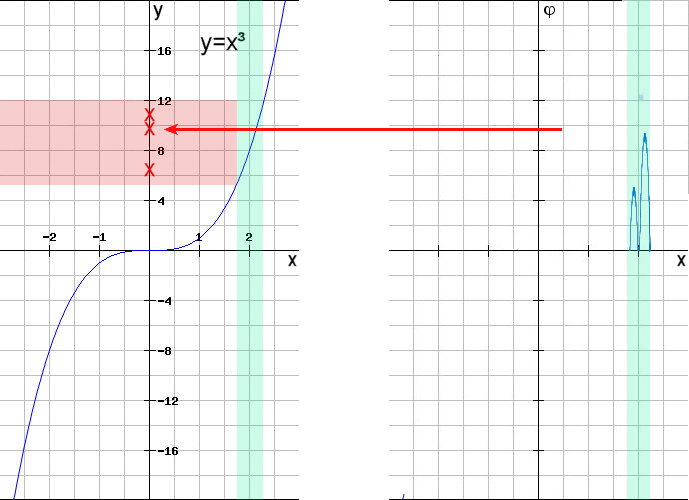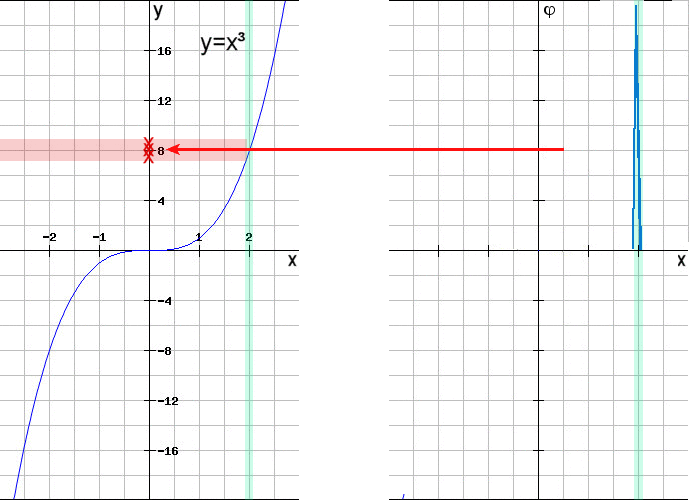
0 erhält man eine Folge von
Zwischenwerten

A
und aufgrund der Stetigkeit der Funktion f gilt
f(Zwischenwerten)

f(A).
Damit kann man die Zuordnung von x zu f(x) zurückbekommen.
Es ist eine andere Art die Funktion zu beschreiben.
Dies führt zu folgender Definition:

Es gibt hierbei keine Beziehung zwischen x und y mehr, sondern eine Beziehung zwischen Testfunktionen aus

und y. Man bezeichnet dies als Distributionen und nicht als Funktionen, obwohl es vielleicht nur eine andere Beschreibung für das "Wesen der Funktion" ist. Und um die Verständlichkeit zu verbessern übernimmt man für die Distributionen auch die Schreibweise der Funktionen.

Mit Distributionen läßt sich die Dirac-Delta-Funktion

(x) definieren.

Gibt man einen x-Wert A

0 vor so kann man für 0<v<|A|/2 Intervalle (A-v,A+v) betrachten. Dann wählt man Testfunktionen

die außerhalb dieser Intervalle 0 sind. Für diese gilt stets

(0)=0 insbesondere auch wenn v

0. Daher besteht eine Verbindung von der Distribution (:

(x):) zu der Funktion

(x) für die man weiß daß

(x)=0 sofern x

0. Es bleibt bei der Spekulation

(0)=7=0=jede beliebige positive Zahl oder

∞.
Das ist unerheblich denn die Distribution hat als Definitionsbereich

und keine x-Werte. Für jedes Element des Definitionsbereiches

ist die Distribution definiert.

Für Distributionen läßt sich die Ableitung einfach über die Ableitung der Testfunktionen erklären:

Es sei hier angemerkt daß dieses Vorgehen doch nicht ganz so einfach ist. Würde man etwa als Raum der Testfunktionen

wählen, also Testfunktionen mit Flächeninhalt 7 anstatt Flächeninhalt 1, so würde die dann aus f entstehende Distribution nach obiger Argumentation mit der Funktion 7f korrespondieren (andere Werte für den Flächeninhalt entsprechend). Also nimmt

eine Sonderstellung ein. Bei der Definition der allgemeinen Ableitung wird aber -

' verwendet die kein Element von

mehr ist. Man müßte also den Raum der Testfunktionen erweitern (nichtnegativ und vorgegebener Flächeninhalt 1 müßten aufgegeben werden). Dann würde aber die Ableitung der Distribution nicht mehr mit der Ableitung der Funktion korrespondieren. Dazu müßte man nachträglich den Definitionsbereich wieder auf

einschränken. Vielleicht ist dies die Problematik der Renormierung bei den Physikern.

Wir gehen hier einmal davon aus daß für

aus

der Ausdruck
T(-

') "sinnvoll berechnet werden kann" (siehe auf dieser Seite weiter unten).
Insbesondere ergibt sich daß jede Distribution beliebig oft differenzierbar ist. Ein Beispiel

Anschaulich kann man sagen daß an der Stelle x=0 die

(x)-Funktion einen Nadelpeak hat der die Sprunghöhe der unstetigen Funktion herausfiltert. Ist der Multiplikationsfaktor positiv so liegt ein Sprung von links unten nach rechts oben vor, ist der Multiplikationsfaktor negativ so liegt ein Sprung von links oben nach rechts unten vor. Die erste Ableitung einer Distribution hat also eine ganz andere Bedeutung als die erste Ableitung einer Funktion die die Tangentensteigung bestimmt. Ist allerdings die Funktion differenzierbar so stimmt die Ableitung der Distribution mit der Ableitung der Funktion überein.

Um übersichtlich arbeiten zu können werden einige Definitionen eingeführt. Man braucht rechtsseitigen und linksseitigen Funktionswert und eine an den Punkt a verschobene

(x-a)-Funktion die den Nadelpeak an der Stelle x-a=0 hat. Dies erleichtert das Verständnis, denn sonst müßte man für jedes a eine eigene Distribution erklären (evtl. durch einen Index).

Damit läßt sich die Ableitung vieler (auch unstetiger) Funktionen im Sinne der Distributionen aufschreiben

Beispiel-Sprungfunktion

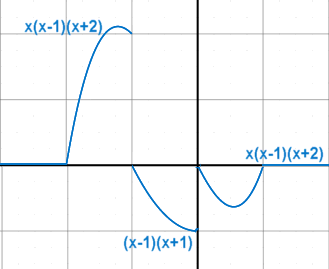
Diese Funktion ist nicht stetig, aber im Sinne der Distributionen beliebig oft differenzierbar. Mit der Treppen-Funktion läßt sich die Funktion in einer Zeile aufschreiben - ein Intervall nach dem anderen

Innerhalb der Intervalle wird natürlich die Tangentensteigung beschrieben.
Existiert f(a+) aber nicht, so definiert man die Distributionsableitung durch obigen Ausdruck indem man f(a+)=0 setzt. Entsprechend bei f(b-) . Da in diesen Fällen kein rechtseitiger bzw. linksseitiger Grenzwert existiert, gibt es kein sinnvolles Ergebnis und der "Problempunkt" wird ausgegrenzt.
Es ist ähnlich wie bei dem Teilen durch 0 was auch verboten wird.
Damit kann man auch folgende Funktionen berücksichtigen.

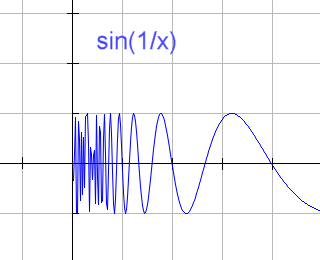
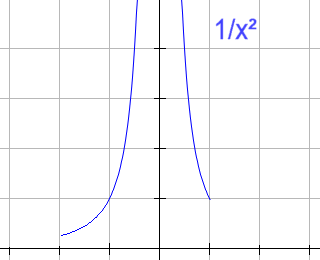
Also
H_(0,2)(x) sin(1/x)
H_(-2,0)(x) 1/x² + H_(0,1)(x) 1/x²

Berechnet man bei diesen Beispielen aber die Integrale über
Funktion x Testfunktion
so steht man vor der Problematik von divergenten Integralen.
Diese Integrale werden dann durch Cauchy-Hauptwert oder Hadamard-Hauptwert so modifiziert daß sich die unendlich hohe Sprunghöhe herausrechnet.

Nun wurde der Begriff der Funktion anders gefaßt. Es stellt sich die Frage nach dem Abstand jetzt für Distributionen. Was bedeuted es zu sagen daß zwei Distributionen nahe sind. Was bedeuted es zu sagen daß sich eine Folge von Distributionen an eine andere Distribution annähert. Da die Distributionswerte reelle Zahlen sind kann man einfach auf den Abstand für reelle Zahlen zurückgreifen.
Sei a>0 eine reelle Zahl und T_a eine Folge von Distributionen. Dann gilt für eine Distribution T

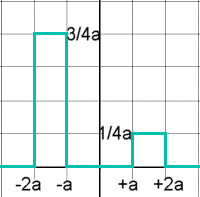
Damit hat man eine Folge von Funktionen (mit Flächeninhalt 1) die gegen die Dirac-Delta-Funktion konvergiert. Allerdings ist keines der Folgen-Elemente eine gerade Funktion, so daß es schwierig zu verstehen ist warum die Dirac-Delta-Funktion eine gerade Funktion sein soll.

Auch ist jedes Folgen-Element in einem ganzen Intervall (-a,+a) identisch 0 . Daher ist es schwierig sich vorzustellen daß die Dirac-Delta-Funktion (die außerhalb Nullpunkt generell 0 ist) im Nullpunkt so stark gegen unendlich geht daß der Flächeninhalt bei 1 bleibt. Solche Vorstellungen sind nur bedingt hilfreich. Der Definitionsbereich der Dirac-Delta-Distribution besteht eben nicht aus x-Werten sondern aus Testfunktionen.

Leichte Änderung

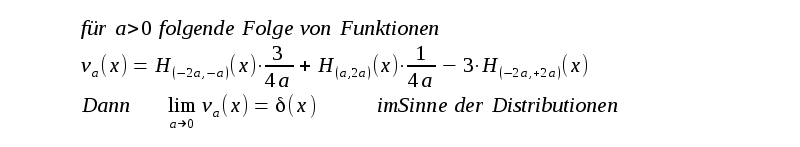
Damit hat man eine Folge von Funktionen von denen keines der Folgen-Elemente den Flächeninhalt 1 hat (für a<1/12 wird der Flächeninhalt positiv), die aber den Flächeninhalt 1 immer mehr annähern. Jedes Folgen-Element ist in einem ganzen Intervall (-a,+a) identisch -3 .

Leichte Änderung

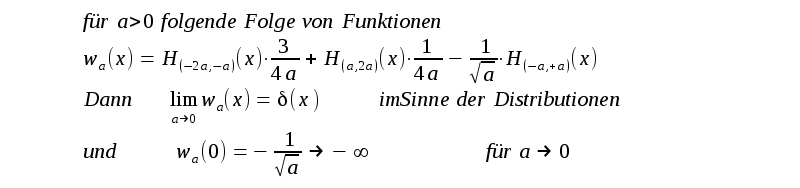
Damit hat man eine Folge von Funktionen deren Negativwert im 0-Punkt über alle Grenzen anwächst für a -> 0 .

Dies kann man schnell erweitern.
Sei u eine stetige Funktion mit u(x)>0 für jedes reelle x.

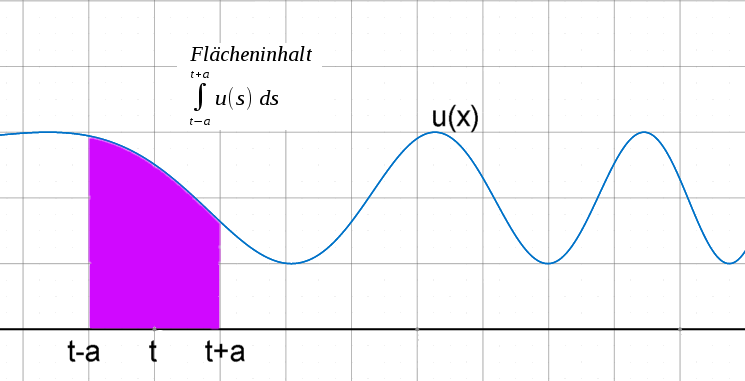
Damit ist u(x) auf jedem Intervall integrierbar mit endlichem Flächeninhalt. Und mit der Treppenfunktion kann man einfach Funktionenfolgen ausschneiden
mit Flächeninhalt 1.

Und natürlich kann man noch weitaus mehr Folgen finden die gegen die Dirac-Delta-Funktion konvergieren - im Sinne der Distributionen.

Nun kann man sich vorstellen daß die Dirac-Delta-Funktion sich räumlich verändert wenn man ein Zeitintervall betrachtet. Dann gibt es einen Zeitparameter t und eine zeitabhängige Dirac-Delta-Funktion

(x-f(t))
Ist die Funktion f stetig so ist auch die Raumverschiebung der zeitabhängigen Dirac-Delta-Funktion "stetig", denn für a -> 0
(:

(x-f(t+a)):)(

(f(t+a)) ->

(f(t))=(:

(x-f(t)):)(

)
Die Testfunktionen geben die Eigenschaften der Funktion f an die Distribution weiter. Damit kann man auch die Ableitung nach dem Zeitparameter aufschreiben.

Und es gibt einen anderen Zugang zur Ableitung einer Distribution.

Damit ist der Satz
Wir gehen hier einmal davon aus daß für

aus

der Ausdruck
T(-

') "sinnvoll berechnet werden kann".
überflüssig geworden denn T(-

') braucht nicht mehr gebildet zu werden.

Eine zusammenfassende Bemerkung zu

Zunächst muß man eine Funktion definieren z.B.

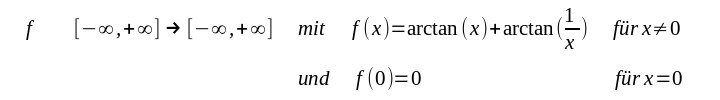
Diese Funktion f ist im klassischen Sinne differenzierbar wenn man den Nullpunkt ausschließt. Strenggenommen darf man aber nicht schreiben

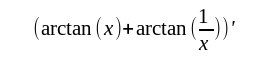
da dieser Ausdruck der Wert der Funktion f an der Stelle x ist. Also ein ganz bestimmter Funktionswert und dieser ist nicht differenzierbar. Trotzdem weiß eigentlich jeder dass damit die Ableitung der Funktion f gemeint ist. Und so ist es auch im Distributionensinn. Hier bedeuted es die Distributionsableitung der regulären Distribution die durch f erzeugt wird. Eine andere Sinngebung ist eigentlich nicht möglich und die Schreibweise verdeutlicht sofort welche Funktion f gemeint ist. Trotzdem gibt es weiterhin Unklarheiten. Definiert man den Wert im Nullpukt anders, z.B. mit der Funktion

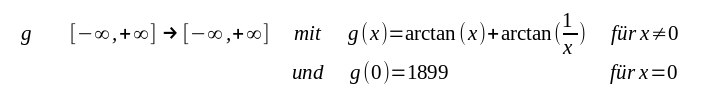
dann sind die Funktionen f und g nicht gleich, aber beide erzeugen die gleiche reguläre Distribution. Nun kann man meinen daß der Wert einer Funktion in einem einzelnen Punkt nicht entscheidend für das Verhalten der abstrakten Funktion ist. Aber die

(x)-Funktion die auf einem Bereich der x=0 nicht enthält mit der Nullfunktion korrespondiert hat man auch nur einen einzelnen Punkt indem sich

(x)-Funktion und Nullfunktion unterscheiden. Die Physiker benutzen die

(x)-Funktion um physikalische Vorgänge zu beschreiben die sich im Nullpunkt konzentrieren.

Die

(x-a)-Funktion ist jedoch keine Funktion und kann keine Zahlen als x-Werte annehmen. Es ist eine symbolische Schreibweise die bedeuted daß in einem Intervall das x=a nicht enthält diese Distribution mit der Nullfunktion korrespondiert und dass die korrespondierende "Stammfunktion" an der Stelle x=a eine Sprunghöhe besitzt. Von daher ist das Argument x mit einem Sinn belegt.

Die Mathematiker wollen ein formal einwandfreies Gedankengebäude und nehmen einen Testfunktionenraum ohne die Einschränkung von nichtnegativ und ohne Flächeninhalt=1 . Dann kann man die Ableitung einer Distribution T gut definieren über

Die Physiker möchten den Zusammenhang von Funktion und Distribution und stützen sich auf das Integral das den von Funktionen erzeugten Distributionen zugrundeliegt.

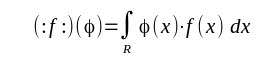
Diese Schreibweise wird auch für die Delta-Distribution verwendet obwohl hier dem Integral keine exakte Bedeutung zukommt, denn die Delta-Distribution ist nicht integrierbar.

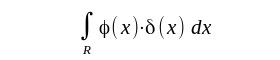
Analog den Regeln für Integrale werden dann formale Regeln für die Delta-Distribution entwickelt obwohl hier doch keine Integrierbarkeit vorliegt.

Ein Beispiel dazu ist

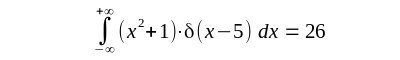
Zunächst muß man sich fragen was die Multiplikation einer Funktion (Definitionsbereich reelle Zahlen) mit einer Distribution (Definitionsbereich Testfunktionen) bedeuten soll. Auch die Bedeutung der Multiplikation zweier Distributionen ist unklar. Die Integrierbarkeit eines solchen Objektes ist ebenfalls nicht erklärt.

Die Physiker benutzen bekannte Mathematik-Regeln und verwenden diese "analog". Eine Sinngebung wäre folgendermaßen möglich:

Wenn für die Funktionen Differenzierbarkeit und lokale Integrierbarkeit vorliegen so gilt für die reguläre Distribution erzeugt von g^.h

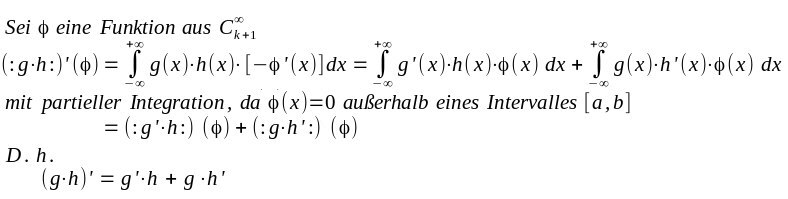
Im Sinne der Distributionen. Also eine Beziehung für die regulären Distributionen erzeugt von den Funktionen g^.h g'^.h g^.h'

Sofern die Funktion f im klassischen Sinne differenzierbar ist, sowie f und f' lokal integrierbar sind, stehen rechts die regulären Distributionen erzeugt von den Funktionen f^.H und f'^.H. Damit wäre die Multiplikation einer Funktion mit der Delta-Distribution sinnvoll als Distribution erklärt.
Integrierbar ist dieses Objekt allerdings immer noch nicht. Aber man kann sich an die grundlegende Eigenschaft für Integrale erinnern

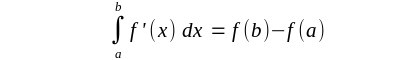
Hat man jetzt eine Distribution die von einer Funktion f erzeugt wird für die
f(b) und f(a) sinnvoll existieren
(z.B. durch stückweise stetige Funktionen für die an den Unstetigkeitsstellen rechtsseitiger und linksseitiger Grenzwert existieren)
so kann man das "Integral für Distributionen" DEFINIEREN über diesen Ausdruck.

Und damit kann man rechnen

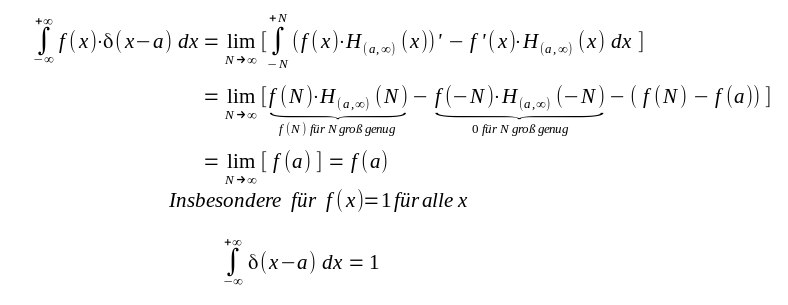
Damit wäre die Gleichheit

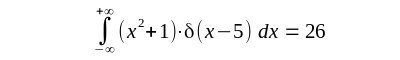
nachgewiesen. Man kann auch nachrechnen

Die andere Möglichkeit zur Definition ist die Annäherung durch eine Folge von Flächeninhalten. Man denke an die irrationalen Zahlen die niemals exakt berechnet werden können - aber man kann sie durch Bruchzahlen beliebig genau annähern. Also nimmt man eine Folge von integrierbaren Funktionen deren reguläre Distributionen gegen

(x-a) konvergieren. Dann definiert man den Flächeninhalt der Distribution als Grenzwert der Flächeninhalte der Funktionen die die regulären Annäherungs-Distributionen erzeugen.
Dazu kann man die Funktionen

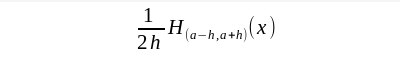
verwenden. Es ergibt sich:

Damit steht der Annäherungs-Flächeninhalt schon fest. Es bedeuted

schlicht die Definition eines sonst völlig unklaren Ausdruckes.

Stammfunktionen:
Zunächst kann man folgende Funktion betrachten

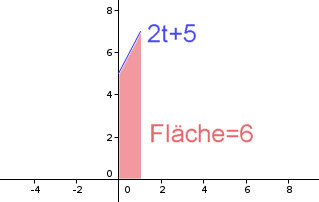
Wie sieht für diese Funktion die Stammfunktion aus?
Eine Stammfunktion bestimmt sich durch

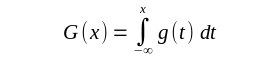
Da für t<0 g(t)=0 gilt, sollte auch für x<0 G(x)=0 gelten.
Also für x<1

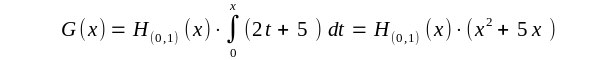
Ist aber 1<x so berechnet G(x) den kompletten Flächeninhalt.

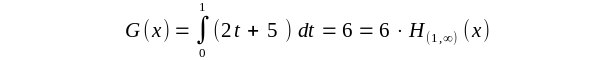
Damit ergibt sich eine Stammfunktion

Ist G(x) eine Stammfunktion so ist auch immer G(x)+C eine Stammfunktion für jede Zahl C

Im Allgemeinen ist die Funktion G nicht im klassischen Sinne differenzierbar.
Versteht man g als reguläre Distribution so ist auch G eine reguläre Distribution. Und mit der Ableitung für Distributionen ergibt sich
G'(x)=H_(a,b)(x)^.u(x)+0^.

(x-a)-G₀^.

(x-b)+G₀^.

(x-b)=g(x)
im Sinne der Distributionen.

Und mit dem obigen (formalen) Integralbegriff kann man auch Stammfunktionen für Distributionen berechnen - vielleicht besser als Stammdistributionen bezeichnet.
Dazu wird die Ableitung der obigen Beispiel-Sprungfunktion benutzt

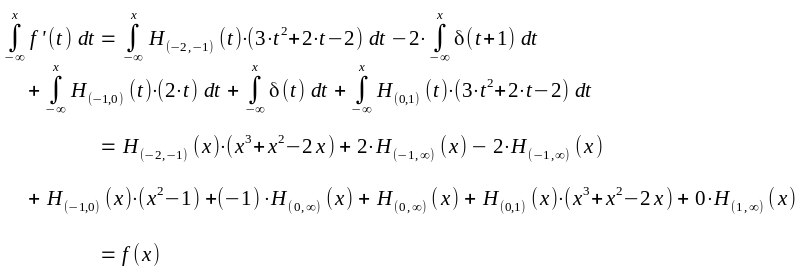
im Sinne der Distributionen

Noch eine Anmerkung zu dem formalen Integralbegriff für eine Distribution die von einer stückweise stetigen Funktion f erzeugt wird:

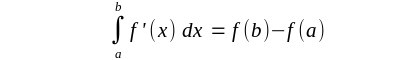
Es wurde gefordert daß f(b) und f(a) sinnvoll existieren. Dies ist an einer Unstetigkeitsstelle aber nicht gegeben.
f(Unstetigkeitsstelle)
ist völlig unklar und für die Distribution die von der Funktion f erzeugt wird auch ganz bedeutungslos. Daher existiert das folgende Integral NICHT:

Ein Rechnen damit führt zu Widersprüchen

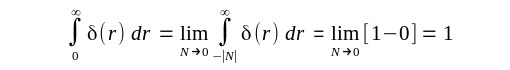
Aber auch

Für Physiker ist die Delta-Funktion eine gerade Funktion und folglich berechnen sie auch 1/2

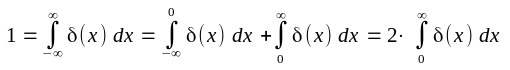
Dieses Integral ist physikalisch von zentraler Bedeutung für kugelsymmetrische Berechnungen, wobei dann x=r der Radius ist.
Allerdings gilt für jedes noch so kleine N>0.

Physikalisch kann man nicht nachprüfen ob sich ein Objekt genau bei r=0 befindet.
Man kann nur sagen daß ein Objekt sehr nahe bei r=0 zu finden ist.