|
Beispiel Deltadistribution Rollwagen Man sollte die vorhergehende Seite Mathematik Distributionen gelesen haben.Ein einfaches pysikalisches Gedankenmodell. Es stehe auf einer Schiene ein Rollwagen der sich reibungsfrei bewegen kann. Entlang der Schiene wähle man ein Koordinatensystem mit Richtung x. Der Ort des Wagens ist also in der Zeit t beschrieben durch x(t) - er kann stillstehen oder rollen. Natürlich gibt es zu jeder Zeit t einen Ort x(t), d.h. x(t) muß eine Funktion sein. Seine Geschwindigkeit ist x'(t) und seine Beschleunigung ist x''(t). Man wähle einen Zeitpunkt t=0 bei dem die Beobachtung des Rollwagens beginnt, dann ist x'(0)=vo die Anfangsgeschwindigkeit und x(0)=xo der Anfangsort. Wird der Wagen jetzt mit einem Hammer in Richtung des Schienenverlaufes geschlagen, zum Zeitpunkt t=a>0 , so liegt eine punktförmige Kraft mit der Stärke K vor. Aber zu anderen Zeiten soll keine weitere Kraft auf den Wagen wirken. Die Kraft des Wagens ist Masse m mal Beschleunigung und natürlich muß ein Kräftegleichgewicht bestehen: |
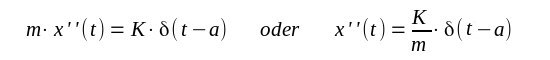
| Diese Gleichungen sind natürlich im Sinne der Distributionen zu verstehen. Die Stammfunktion oder besser Stammdistribution ist bis auf eine Konstante Zahl C bestimmt durch |

| Auch diese Gleichung ist natürlich im Sinne der Distributionen zu
verstehen. Allerdings stehen auf der rechten Seite reguläre
Distributionen, also erzeugt von Funktionen - also muß auch x'(t)
von einer Funktion erzeugt werden. Damit ist diese Gleichung
auch im Sinne der Funktionen zu verstehen. Und dies bedeuted daß
man t-Werte einsetzen kann (bei Distributionen kann man keine Zahlenwerte
eingeben). Für t=0 erhält man C=vo Und da Funktionen vorliegen kann man diese auch in einem Koordinatensystem sichtbar machen. |
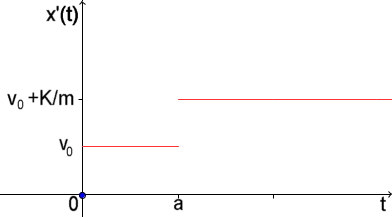
| Dies ist für den Fall K>0 gezeichnet worden. Es bedeuted daß die Anfangsgeschwindigkeit nach dem Zeitpunkt a um K/m erhöht worden ist - ein Hammerschlag in Richtung der Anfangsgeschwindigkeit. Diese Funktion ist nicht im klassischen Sinne differenzierbar. Allerdings als Funktion integrierbar und damit wieder in einem Koordinatensystem sichtbar darstellbar. |
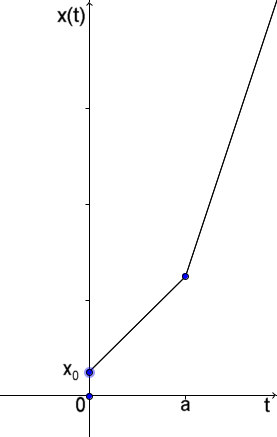
| Die Lösung wäre also x(t)= H(0,a)(t).[vo.t+xo] + H(a,∞)(t).[(vo+K/m).t+xo-aK/m] Diese Funktion ist nicht im klassischen Sinne differenzierbar. Also muß man diese wieder im Sinne der Distributionen verstehen. Dann ist x'(t)= xo. + H(a,∞)(t).[vo+K/m] = xo. und x''(t)=xo. =xo. Dies ist die Ausgangs-Differentialgleichung wenn man von den ersten beiden Delta-Distributionen absieht. Diese beschreiben die Anfangsbedingungen zur Zeit t=0 im Distributionensinne. Dieses Modell soll jetzt verbessert werden. Denn bei einem realen Rollwagen gibt es Reibung von Räder/Schiene, Reibung von Achse/Lager, Luftwiderstand evtl. durch Wind, nicht waagrecht verlegte Schienen ... Daher wird eine geschwindigkeitsabhängige Reibungskraft R berücksichtigt: |
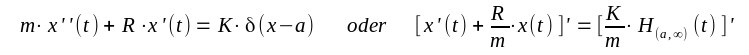
| Diese Gleichungen sind natürlich wieder im Sinne der Distributionen zu verstehen. Die Stammfunktion oder besser Stammdistribution ist bis auf eine Konstante Zahl C1 bestimmt durch |
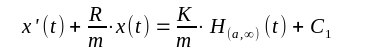
| Auch diese Gleichung ist natürlich im Sinne der Distributionen zu verstehen. Allerdings steht auf der rechten Seite eine reguläre Distributionen, also erzeugt von einer Funktion und auch die Lösung x(t) soll von einer Funktion erzeugt werden, denn man erwartet daß es zu jedem Zeitpunkt t einen Ort x(t) für den Rollwagen gibt. Also muß auch x'(t) von einer Funktion erzeugt werden. Damit ist diese Gleichung auch im Sinne der Funktionen zu verstehen. Und dies bedeuted daß man t-Werte einsetzen kann. Und diese Gleichung zerfällt in zwei Gleichungen für unterschiedliche t-Intervalle: |
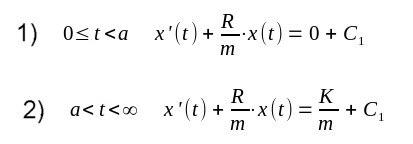
| Die allgemeine Lösung von 1) ergibt sich mit einer Konstanten C2 |
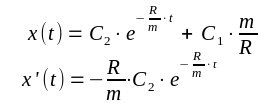
|
Die Konstanten bestimmt man durch die Anfangsbedingungen x'(0)=vo die Anfangsgeschwindigkeit und x(0)=xo der Anfangsort. Man erhält für die Geschwindigkeit |
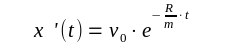
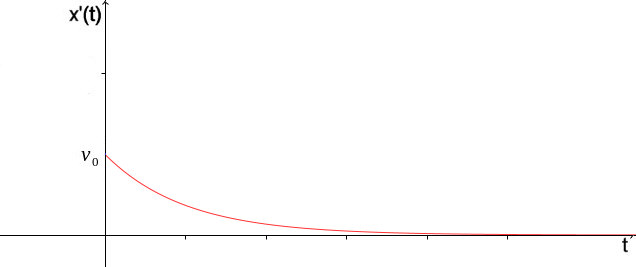
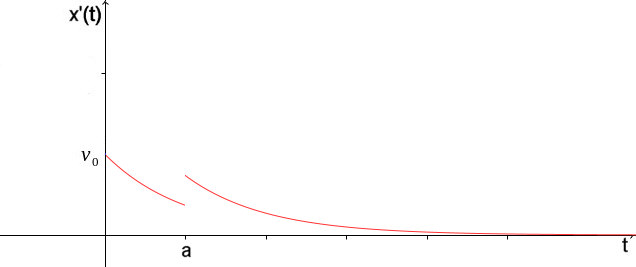
| Dies ist ein exponentieller Abfall, die Geschwindigkeit wird schnell
zu 1mm/Stunde, dann 1mm/Tag, dann 1mm/Monat. Der Rollwagen bleibt stehen,
eine Geschwindigkeit ist nicht mehr meßbar. Für den Ort des Rollwagens erhält man |
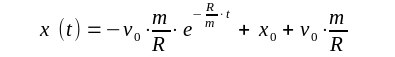
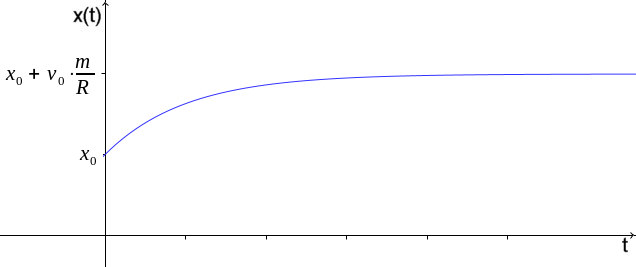
| Die maximale Entfernung des Rollwagens ist also xo+vom/R und der Abstand
zu dieser maximalen Entfernung wird schnell 10cm, dann 1cm, dann 1mm,
dann .... Ist der Zeitpunkt des Hammerschlages nicht im Beobachtungszeitraum, z.B. a=6Monate, so wird die Realität gut beschrieben. Erfolgt der Hammerschlag im Beobachtungszeitraum so ist auch die Gleichung 2) zu berücksichtigen. Die allgemeine Lösung für 2) lautet |
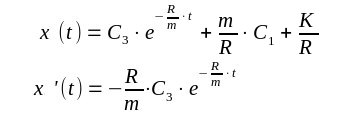
| Es ist noch die Konstante C3 zu berechnen. Dazu berücksichtigt
man daß der Rollwagen nicht teleportieren kann, die Ortsfunktion muß
stetig sein. Also x1) (a-)=x2) (a+) |
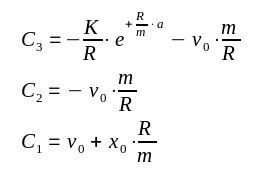
| Man erhält für die Geschwindigkeit |
| Für den Ort des Rollwagens erhält man |
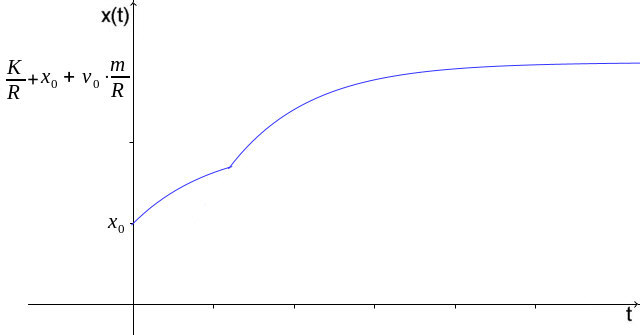
| Die Kraft K des Hammerschlages erhöht die maximale Entfernung des
Rollwagens. Eine Anmerkung für Physiker: Die Dimension von K/m ist Meter/Sekunde2 Die Dimension von H(a,∞)(t) ist Sekunde Daher hat in Gleichung 2) K/m nur noch die Dimension Meter/Sekunde Eigentlich sollte man hier schreiben (Dimension der Zeit).K/m Von daher hat K/R im letzten Schaubild die Dimension Meter. |