|
Beispiel Deltadistribution Wachstumsprozess Man sollte die vorhergehende Seite Mathematik Distributionen gelesen haben.Es sei eine nachwachsende Kultur gegeben, die eine Wachstumsrate von 8% besitzt. Der Anfangsbestand der Kultur sei A. Nach einer Zeitdauer (Stunde, Tage, Monate ..) wird eine Menge N entnommen. Nach weiteren drei Zeitdauern wird wieder eine Menge N entnommen. Nach insgesamt 8 Zeitdauern soll wieder der Anfangsbestand A der Kultur vorliegen. Damit wird ein nachhaltiger Verbrauch der Kultur sichergestellt. Welche Menge N ist möglich? Es sei p(t) der Bestand der Kultur zur Zeit t (in Stunden, Tagen, Monaten, ..). Die Änderung des Bestandes p'(t) bestimmt sich durch Zuwächse aufgrund der Wachstumsrate minus Entnahmen. Der Anfangsbestand kann als einmaliger Zuwachs zur Zeit t=0 aufgefasst werden. |
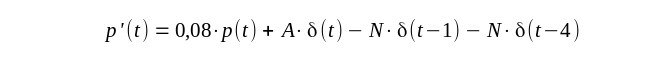
| Diese Gleichung ist natürlich im Sinne der Distributionen zu verstehen. Und für die Stammdistribution von p'(t) - 0,08 p(t) ergibt sich |
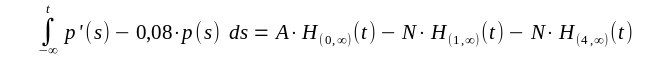
| Auch diese Gleichung ist natürlich im Sinne der Distributionen zu verstehen. Da rechts reguläre Distributionen stehen ist auch die Stammdistribution von einer Funktion erzeugt worden. Damit kann man t-Werte einsetzen und diese Gleichung zerfällt in drei Gleichungen für unterschiedliche t-Intervalle |

| Auf den Intervallen (0,1) und (1,4) und (4,∞) gilt die Gleichung p'(t) - 0,08 p(t) = 0 im Sinne der Funktionen. Diese Gleichung wird von einer e-Funktion erfüllt. Die Lösungsfunktion also |
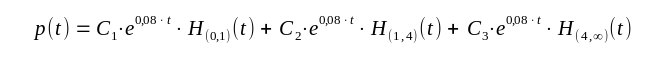
| Es sind noch die Konstanten zu bestimmen. Dazu bildet man für die
reguläre Distribution erzeugt von der Lösungsfunktion p'(t) - 0,08 p(t) |
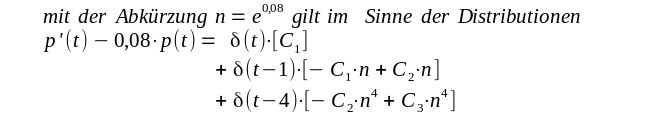
| Dies vergleicht man mit der zu Beginn aufgestellten Differentialgleichung |

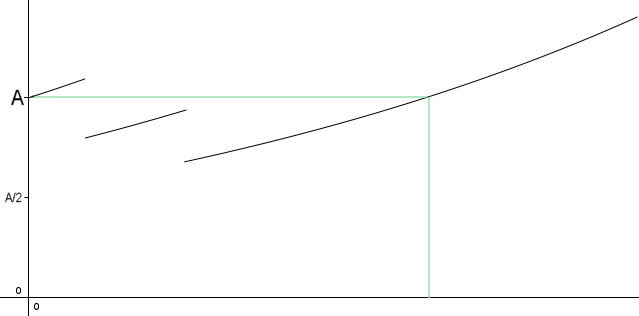
| Damit ist die Lösungsfunktion bestimmt: |
|
Der Bestand der Kultur nach den zwei Entnahmen wird beschrieben durch den
Term mit der Konstanten C3. Es ist der Bestands-Wert für t=T (mit T=8) gesucht und dieser soll wieder A sein, der Anfangsbestand. Man erhält |
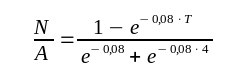
|
Für T=8 (8 Zeitdauern seit Beginn) erhält man: Erlaubt man der Kultur nach den beiden Entnahmen eine Ruhephase von 4 Zeitdauern sollte die Entnahmemenge N 28,66% von A (dem Anfangsbestand) sein. Eine größere Entnahme führt zu einer Verkleinerung der Kultur. Eine kleinere Entnahme führt zu einem Wachsen der Kultur. Für T=6 (6 Zeitdauern seit Beginn) erhält man: Erlaubt man der Kultur nach den beiden Entnahmen eine Ruhephase von 2 Zeitdauern sollte die Entnahmemenge N 23,11% von A (dem Anfangsbestand) sein. Für T=10 (10 Zeitdauern seit Beginn) erhält man: Erlaubt man der Kultur nach den beiden Entnahmen eine Ruhephase von 6 Zeitdauern sollte die Entnahmemenge N 33,39% von A (dem Anfangsbestand) sein. |