|
Beispiel Deltadistribution Delta-Rechnen Man sollte die vorhergehende Seite Mathematik Distributionen gelesen haben.Die Multiplikation einer Funktion mit der Delta-Distribution wurde analog der Produktregel beim Differenzieren definiert über (sofern die Funktion f im klassischen Sinne differenzierbar ist und f und f' lokal integrierbar sind) |
![]()
| Damit kann man direkt mit Distributionen rechnen |
![]()
| Auch die Multiplikation einer Funktion mit der Ableitung der Delta-Distribution kann man analog der Produktregel beim Differenzieren definieren über (sofern die Funktionen f und f' im klassischen Sinne differenzierbar sind und f und f' und f'' lokal integrierbar sind) |
![]()
| Auch hier stehen rechts bereits Terme die (nach oben) als Distributionen bekannt sind. Und auch hier kann man rechnen |
![]()
| Die Produktregel ist also zentral für ein Delta-Rechnen. Es wurde auf der Distributionen-Startseite bereits gezeigt |
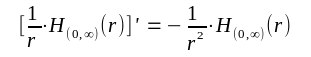
| Da bei 0 kein rechtseitiger Grenzwert existiert wird die unendlich hohe Sprunghöhe auf 0 gesetzt. Dieses Ergebnis kann man auch mit Delta-Rechnen erhalten: |
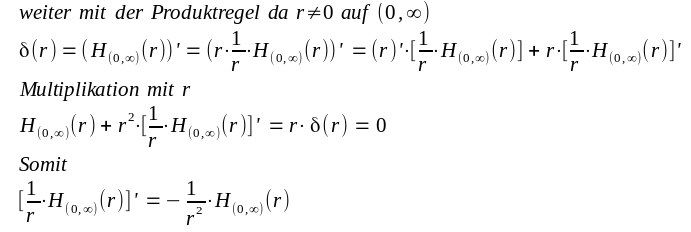
| Man kann also ganz ohne Integrale oder Testfunktionen auskommen. Auch bei der folgenden physikalisch zentralen Fragestellung |


|
Distributionen wurden entwickelt um die Ableitung von Funktionen zu
verallgemeinern. Mit Distributionen kann man stückweise stetige
Funktionen differenzieren und die Sprunghöhe an den Unstetigkeitsstellen
bestimmen. Aber schon bei Funktionen hat man das Problem dass man nicht durch 0 teilen darf. Eine Funktion f(r)=1/r kann man erst sinnvoll aufschreiben wenn das Teilen durch 0 vermieden wird. Hier ist die Treppenfunktion eine elegante Möglichkeit Funktionen für alle reellen Zahlen aufzuschreiben: |
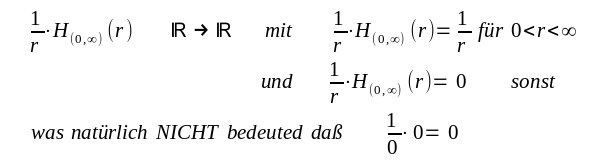
| Die Einführung von Distributionen erfordert aber die lokale Integrierbarkeit. Und dies ist bei dieser Funktion nicht gegeben. Es sei denn man ändert den Integralbegriff ab durch die Einführung von Cauchy-Hauptwert oder Hadamard-Hauptwert. Nur dadurch kann man diese Funktion in das Schema der Distributionen hineinzwingen. Eine Aussage der Form |
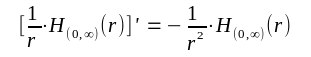
| ist im Sinne der Distributionen eigentlich nicht möglich. Aber die Distributionen sollten doch die Ableitung von Funktionen verallgemeinern. Und die Möglichkeit eine unendlich hohe Sprunghöhe zu vermeiden sollte auch als sinnvolle Verallgemeinerung der Ableitung für Funktionen angesehen werden. |
|
Noch eine Bemerkung zur Multiplikation bei Distributionen. Distributionen haben als Definitionsbereich Testfunktionen. Wird die Distribution aber von einer Funktion erzeugt so kann man diese Funktion mit anderen Funktionen multiplizieren und aus diesem Produkt wieder eine Distribution erzeugen. Daher macht die Definitionen |
![]()
| Sinn wenn die Funktion f im klassischen Sinne differenzierbar ist und f und f' lokal integrierbar sind. Ist aber die Funktion nicht im klassischen Sinne differenzierbar, z.B. |
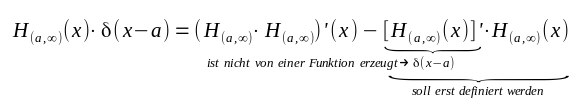
|
so ist diese Schreibweise unsinnig und ergibt keine Definition. Ein solches Produkt |
![]()
| ist hier nicht erklärt und genauso unsinnig wie |
![]()